题目内容
函数f(x)=ax3+bx2+cx+d(a≠0),若a+b+c=0,导函数f′(x)满足f′(0)f′(1)>0,设f'(x)=0的两根为x1,x2,则|x1-x2|的取值范围是
- A.
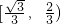
- B.
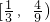
- C.
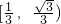
- D.
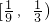
A
分析:先求出f′(x)=3ax2+2bx+c,可得 =
=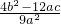 =
=
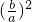 +
+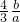 +
+ ,由f′0)•f′(1)>0,
,由f′0)•f′(1)>0,
解得-2< <-1,利用二次函数的性质求出
<-1,利用二次函数的性质求出 的范围,即可求得|x1-x2|的取值范围.
的范围,即可求得|x1-x2|的取值范围.
解答:由题意得:f′(x)=3ax2+2bx+c,∵x1,x2是方程f′(x)=0的两个根,
∴x1+x2=-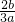 ,x1•x2=
,x1•x2=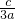 .∴|x1-x2|2 =
.∴|x1-x2|2 =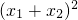 -4x1x2 ,
-4x1x2 ,
∴ =
=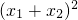 -4x1•x2 =
-4x1•x2 =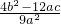 .
.
∵a+b+c=0,∴c=-a-b,
∴ =
=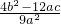 =
=
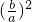 +
+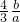 +
+ .
.
∵f′0)•f′(1)>0,f(0)=c=-(a+b),且f′(1)=3a+2b+c=2a+b,∴(a+b)(2a+b)<0,
即2a2+3ab+b2<0,∵a≠0,两边同除以a2得: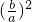 +3
+3  +2<0,解得-2<
+2<0,解得-2< <-1.
<-1.
由二次函数的性质可得,当 =-
=- 时,
时, 有最小值为
有最小值为  ,
,
当 趋于-1时,
趋于-1时, 趋于
趋于  ,故
,故  ∈
∈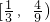 ,
,
故|x1-x2|∈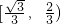 ,
,
故选A.
点评:本题考查根与系数的关系的灵活运用,解题时要认真审题,仔细解答,注意合理地进行等价转化,属于中档题.
分析:先求出f′(x)=3ax2+2bx+c,可得
 =
=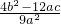 =
=
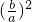 +
+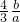 +
+ ,由f′0)•f′(1)>0,
,由f′0)•f′(1)>0,解得-2<
 <-1,利用二次函数的性质求出
<-1,利用二次函数的性质求出 的范围,即可求得|x1-x2|的取值范围.
的范围,即可求得|x1-x2|的取值范围.解答:由题意得:f′(x)=3ax2+2bx+c,∵x1,x2是方程f′(x)=0的两个根,
∴x1+x2=-
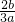 ,x1•x2=
,x1•x2=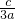 .∴|x1-x2|2 =
.∴|x1-x2|2 =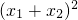 -4x1x2 ,
-4x1x2 ,∴
 =
=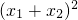 -4x1•x2 =
-4x1•x2 =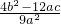 .
.∵a+b+c=0,∴c=-a-b,
∴
 =
=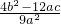 =
=
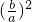 +
+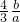 +
+ .
.∵f′0)•f′(1)>0,f(0)=c=-(a+b),且f′(1)=3a+2b+c=2a+b,∴(a+b)(2a+b)<0,
即2a2+3ab+b2<0,∵a≠0,两边同除以a2得:
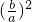 +3
+3  +2<0,解得-2<
+2<0,解得-2< <-1.
<-1.由二次函数的性质可得,当
 =-
=- 时,
时, 有最小值为
有最小值为  ,
,当
 趋于-1时,
趋于-1时, 趋于
趋于  ,故
,故  ∈
∈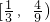 ,
,故|x1-x2|∈
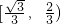 ,
,故选A.
点评:本题考查根与系数的关系的灵活运用,解题时要认真审题,仔细解答,注意合理地进行等价转化,属于中档题.

练习册系列答案
相关题目