题目内容
设数列{an}是等比数列，a1=
，公比q是(x+
)4的展开式中的第二项（按x的降幂排列）.（1）用n,x表示通项an与前n项和Sn；
（2）若An=
,用n,x表示An.
解析：(1)∵a1=，
∴即∴m=3.
由(x+
)4知T2=
x3·
=x,
∴an=xn-1,Sn=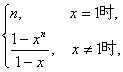
（2）当x=1时，Sn=n，
An=
+2
+3
+…+n
，
又∵An=n
+(n-1) 
+(n-2)
+…+
,
=
, 
=
,…
∴2An=n(
+
+…+
)=n·2n,
∴An=n·2n-1.
当x≠1时，Sn=
.
［(
+
+…+
)-(x
+x2
+…+xn
)］=
［2n-1-(1+x
+x2
+xn
-1)］=
［2n-(1+x)n］.
∴An=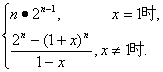
练习册系列答案
相关题目