题目内容
已知圆x2+y2=r2及圆内一点A（a,b）(a、b不同时为零)，求被A平分的弦所在的直线方程.
解析：本题主要考查直线被圆截得的弦长中点问题，可以利用直线参数方程中参数t的性质.首先设出直线的参数方程，代入圆的方程，可以得到关于参数t的二次方程，根据参数的性质可知方程两根的和为0.
解：设所求直线的参数方程为
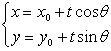
代入圆的方程x2+y2=r2,整理得t2+2(acosθ+bsinθ)t+a2+b2-r2=0.
设t1、t2为方程两根，
∵A是中点，∴t1+t2=0,即acosθ+bsinθ=0.
∴tanθ=-
，即k=-
.
∴所求直线方程是y-b=-
(x-a),即ax+by=a2+b2.
练习册系列答案
相关题目
已知圆x2+y2+2x-4y+1=0关于直线2ax-by+2=0（a，b∈R）对称，则ab的取值范围是（ ）
A、(-∞，
| ||
B、[
| ||
C、(-
| ||
D、(0，
|