题目内容
设A 和G 分别是a，b 等差中项和等比中项，则a2+b2 的值为
- A.2A2-G2
- B.4A2-G2
- C.2A2-2G2
- D.4A2-2G2
D
分析：由A为a与b的等差中项，利用等差数列的性质得到2A=a+b，又G为a与b的等比中项，利用等比数列的性质得到G2=ab，然后把所求式子利用完全平方公式变形后，将表示出的a+b及ab代入，化简后即可得到结果．
解答：∵A和G分别是a，b等差中项和等比中项，
∴2A=a+b，G2=ab，
则a2+b2=（a+b）2-2ab=（2A）2-2G2=4A2-2G2．
故选D
点评：此题考查了等差、等比数列的性质，以及完全平方公式的运用，熟练掌握性质是解本题的关键．
分析：由A为a与b的等差中项，利用等差数列的性质得到2A=a+b，又G为a与b的等比中项，利用等比数列的性质得到G2=ab，然后把所求式子利用完全平方公式变形后，将表示出的a+b及ab代入，化简后即可得到结果．
解答：∵A和G分别是a，b等差中项和等比中项，
∴2A=a+b，G2=ab，
则a2+b2=（a+b）2-2ab=（2A）2-2G2=4A2-2G2．
故选D
点评：此题考查了等差、等比数列的性质，以及完全平方公式的运用，熟练掌握性质是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
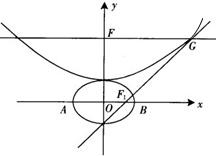设b＞0，椭圆方程为
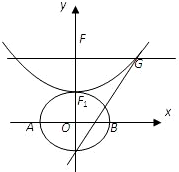设b＞0，椭圆方程为