题目内容
已知函数f(x)=Asin(ωx+φ)的周期为4π,振幅为2,初相为 .求:函数f(x)的解析式及单调区间.
.求:函数f(x)的解析式及单调区间.
解:由已知可得,A=2, (4分)
(4分)
∵周期为4π,∴ ,∴
,∴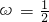
∴ (6分)
(6分)
当 (k∈Z)时,函数f(x)单调递增,(8分)
(k∈Z)时,函数f(x)单调递增,(8分)
解得 (k∈Z)
(k∈Z)
∴函数f(x)的递增区间是 (k∈Z)(9分)
(k∈Z)(9分)
当 (k∈Z)时,函数f(x)单调递减,(11分)
(k∈Z)时,函数f(x)单调递减,(11分)
解得 (k∈Z)
(k∈Z)
∴函数f(x)的递减区间是 (k∈Z)(12分)
(k∈Z)(12分)
分析:根据函数f(x)=Asin(ωx+φ)的周期为4π,振幅为2,初相为 ,可求A、ω、φ的值,从而可得函数f(x)的解析式,利用正弦函数的单调性,即可求得单调区间.
,可求A、ω、φ的值,从而可得函数f(x)的解析式,利用正弦函数的单调性,即可求得单调区间.
点评:本题考查三角函数解析式的确定,考查函数的单调性,考查学生的计算能力,属于基础题.
 (4分)
(4分)∵周期为4π,∴
 ,∴
,∴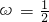
∴
 (6分)
(6分)当
 (k∈Z)时,函数f(x)单调递增,(8分)
(k∈Z)时,函数f(x)单调递增,(8分)解得
 (k∈Z)
(k∈Z)∴函数f(x)的递增区间是
 (k∈Z)(9分)
(k∈Z)(9分)当
 (k∈Z)时,函数f(x)单调递减,(11分)
(k∈Z)时,函数f(x)单调递减,(11分)解得
 (k∈Z)
(k∈Z)∴函数f(x)的递减区间是
 (k∈Z)(12分)
(k∈Z)(12分)分析:根据函数f(x)=Asin(ωx+φ)的周期为4π,振幅为2,初相为
 ,可求A、ω、φ的值,从而可得函数f(x)的解析式,利用正弦函数的单调性,即可求得单调区间.
,可求A、ω、φ的值,从而可得函数f(x)的解析式,利用正弦函数的单调性,即可求得单调区间.点评:本题考查三角函数解析式的确定,考查函数的单调性,考查学生的计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目