题目内容
(本小题满分14分)
指出函数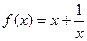 在
在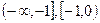 上的单调性,并证明之.
上的单调性,并证明之.
解:任取x1,x2
 且x
且x 1<x2
1<x2 

由x1<x2 —1知x1x2>1, ∴
—1知x1x2>1, ∴ , 即
, 即
∴f(x)在 上是增函数;当1
上是增函数;当1 x1< x2<0时,有0< x1x2<1,得
x1< x2<0时,有0< x1x2<1,得
∴ ∴f(x)在
∴f(x)在 上是减函数.
上是减函数.
再利用奇偶性,给出 单调性,证明略.
单调性,证明略.
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
(本小题满分14分)
指出函数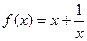 在
在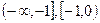 上的单调性,并证明之.
上的单调性,并证明之.
解:任取x1,x2
 且x
且x 1<x2
1<x2 

由x1<x2 —1知x1x2>1, ∴
—1知x1x2>1, ∴ , 即
, 即
∴f(x)在 上是增函数;当1
上是增函数;当1 x1< x2<0时,有0< x1x2<1,得
x1< x2<0时,有0< x1x2<1,得
∴ ∴f(x)在
∴f(x)在 上是减函数.
上是减函数.
再利用奇偶性,给出 单调性,证明略.
单调性,证明略.
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案