题目内容
已知 (-1<x<1).
(-1<x<1).
(1)若f(a)+f(b)=0,求证a+b=0;
(2)设f( )+f(
)+f( )=f(x0),求x0的值;
)=f(x0),求x0的值;
(3)设x1,x2∈(-1,1),是否存在x3∈(-1,1),使得f(x1)+f(x2)=f(x3),若存在,求出x3,并证明你的结论;若不存在,请说明理由。
 (-1<x<1).
(-1<x<1).(1)若f(a)+f(b)=0,求证a+b=0;
(2)设f(
 )+f(
)+f( )=f(x0),求x0的值;
)=f(x0),求x0的值;(3)设x1,x2∈(-1,1),是否存在x3∈(-1,1),使得f(x1)+f(x2)=f(x3),若存在,求出x3,并证明你的结论;若不存在,请说明理由。
解:(1)由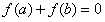 得
得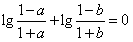
∴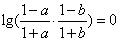
∴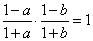
∴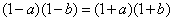
化简得a+b=0;
(2)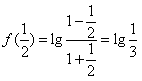 ,
,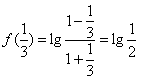 ,
,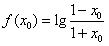
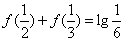
由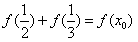 得
得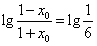
解得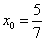 ;
;
(3)假设存在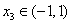 使得
使得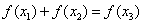
∵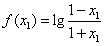 ,
,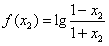
∴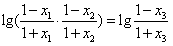
解得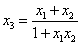
下证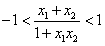
先用分析法证明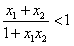
∵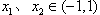
∴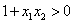
要证明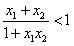 ,即要证
,即要证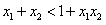 ,即要证
,即要证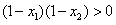
∵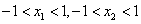
∴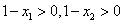
∴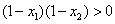
同理可证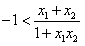
所以存在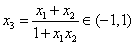 ,使得
,使得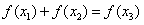 。
。
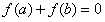 得
得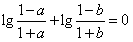
∴
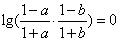
∴
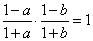
∴
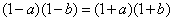
化简得a+b=0;
(2)
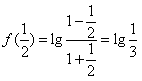 ,
,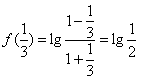 ,
,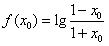
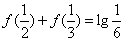
由
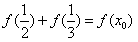 得
得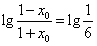
解得
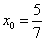 ;
;(3)假设存在
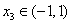 使得
使得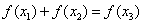
∵
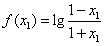 ,
,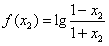
∴
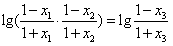
解得
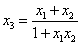
下证
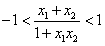
先用分析法证明
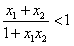
∵
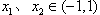
∴
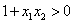
要证明
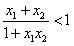 ,即要证
,即要证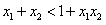 ,即要证
,即要证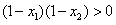
∵
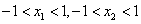
∴
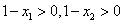
∴
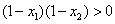
同理可证
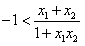
所以存在
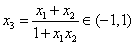 ,使得
,使得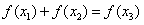 。
。
练习册系列答案
相关题目
 ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个. ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式; .…………………………………………4分
.…………………………………………4分 (n∈N*),bn=
(n∈N*),bn= =
= =
= =
= ,
, -1=
-1= n-1=
n-1= =1-an=1-
=1-an=1- =
= ,
,  +
+ +…+
+…+ +
+ +…+
+…+
 =1-
=1- 已知函数f(x)的定义域为[-2,+∞),部分对应值如下表.f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示.若实数a满足f(2a+1)<1,则a的取值范围是
已知函数f(x)的定义域为[-2,+∞),部分对应值如下表.f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示.若实数a满足f(2a+1)<1,则a的取值范围是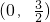



 是增函数,且h(x)的导函数h'(x)存在正零点,求m的值.
是增函数,且h(x)的导函数h'(x)存在正零点,求m的值.