题目内容
(理科)(本小题满分12分)如图分别是正三棱台ABC-A1B1C1的直观图和正视图,O,O1分别是上下底面的中心,E是BC中点.
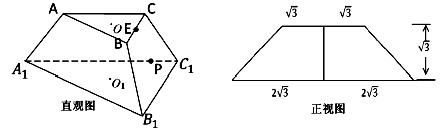
(1)求正三棱台ABC-A1B1C1的体积;
(2)求平面EA1B1与平面A1B1C1的夹角的余弦;
(3)若P是棱A1C1上一点,求CP+PB1的最小值.
(1) ;
;
(2) ;(3)最小值为
;(3)最小值为 。
。
【解析】
试题分析:(1)由题意 ,正三棱台高为
,正三棱台高为 ..2分
..2分
 ..4分
..4分
(2)设 分别是上下底面的中心,
分别是上下底面的中心, 是
是 中点,
中点, 是
是 中点.以
中点.以 为原点,过
为原点,过 平行
平行 的线为
的线为 轴建立空间直角坐标系
轴建立空间直角坐标系 .
.  ,
, ,
,  ,
, ,
, ,
, ,
, ,
,

设平面 的一个法向量
的一个法向量 ,则
,则 即
即
取 ,取平面
,取平面 的一个法向
的一个法向
量 ,设所求角为
,设所求角为
则 ..8分
..8分
(3)将梯形 绕
绕 旋转到
旋转到 ,使其与
,使其与 成平角
成平角

 ,由余弦定理得
,由余弦定理得
即 的最小值为
的最小值为 ..13分
..13分
考点:本题主要考查立体几何中的体积计算、角的计算。
点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤。利用向量则简化了证明过程,对计算能力要求高。

 名校课堂系列答案
名校课堂系列答案(理科)(本小题满分12分)PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095 – 2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 ~ 75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标。从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
|
PM2.5日均值 (微克/立方米) |
[25,35] |
(35,45] |
(45,55] |
(55,65] |
(65,75] |
(75,85] |
|
频数 |
3 |
1 |
1 |
1 |
1 |
3 |
(1)从这10天的PM2.5日均值监测数据中,随机抽取3天,求恰有1天空气质量达到一级的概率;(2)从这10天的数据中任取3天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列;(3)以这10天的PM2.5日均值来估计一年的空气质量状况,则一年(按366天算)中平均有多少天的空气质量达到一级或二级。(精确到整数)
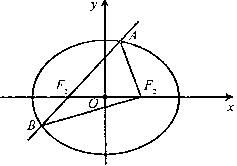 如图,椭圆
如图,椭圆