题目内容

过点C（4，0）的直线与双曲线
x2
4
-
y2
12
=1的右支交于A、B两点，则直线AB的斜率k的取值范围是（　　）
分析：根据题意，设直线AB的方程为y=k（x-4），与双曲线消去y得到关于x的一元二次方程，利用根与系数的关系与根的判别式建立关于k的不等式组，解之即可得到k的取值范围．
解答：解：设A（x1，y1）、B（x2，y2），直线AB的方程为y=k（x-4），
由
y=k(x-4)
x2
4
-
y2
12
=1
消去y，得（3-k2）x2+8k2x-16k2-12=0．
∴x1+x2=-
8k2
3-k2
，x1+x2=
-16k2-12
3-k2
．
∵直线AB与抛物线的右支有两个不同的交点，
∴
△=64k4-4(3-k2)(-16k2-12)＞0
x1+x2=-
8k2
3-k2
＞0
x 1x2=
-16k2-12
3-k2
＞0
，化简此不等式组可得k2＞3，即|k|＞
3
．
故选：B
点评：本题已知经过定点的直线与双曲线右支交于不同的两点，求直线斜率的取值范围．着重考查了双曲线的简单性质、直线与圆锥曲线的位置关系等知识，属于中档题．
练习册系列答案
相关题目
已知动点P与直x=4的距离等于它到定点F（1，0）的距离的2倍，
（1）求动点P的轨迹C的方程；
（2）点M（1，1）在所求轨迹内，且过点M的直线与曲线C交于A、B，当M是线段AB中点时，求直线AB的方程．
已知动点P与直x=4的距离等于它到定点F（1，0）的距离的2倍，
（1）求动点P的轨迹C的方程；
（2）点M（1，1）在所求轨迹内，且过点M的直线与曲线C交于A、B，当M是线段AB中点时，求直线AB的方程．

（本小题满分13分）

        已知椭圆C的中心在的点，焦点在x轴上，F1，F2分别是椭圆C的左、右焦点，M是椭圆短轴的一个端点，过F1的直线与椭圆交于A，B两点，的面积为4，的周长为

   （I）求椭圆C的方程；

   （II）设点Q的从标为（1，0），是否存在椭圆上的点P及以Q为圆心的一个圆，使得该圆与直

线PF1，PF2都相切，若存在，求出P点坐标及圆的方程；若不存在，请说明理由。
已知动点P与直x=4的距离等于它到定点F（1，0）的距离的2倍，
（1）求动点P的轨迹C的方程；
（2）点M（1，1）在所求轨迹内，且过点M的直线与曲线C交于A、B，当M是线段AB中点时，求直线AB的方程．

已知直三棱柱中, , ， 是和的交点, 若.

（1）求的长；  （2）求点到平面的距离；

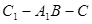（3）求二面角的平面角的正弦值的大小.

【解析】本试题主要考查了距离和角的求解运用。第一问中，利用ACCA为正方形, AC=3

第二问中，利用面BBCC内作CDBC, 则CD就是点C平面ABC的距离CD=，第三问中，利用三垂线定理作二面角的平面角，然后利用直角三角形求解得到其正弦值为

解法一: (1)连AC交AC于E, 易证ACCA为正方形, AC=3 ……………  5分

(2)在面BBCC内作CDBC, 则CD就是点C平面ABC的距离CD= … 8分

(3) 易得AC面ACB, 过E作EHAB于H, 连HC, 则HCAB

CHE为二面角C－AB－C的平面角. ………  9分

sinCHE=二面角C－AB－C的平面角的正弦大小为 ……… 12分

解法二: (1)分别以直线CB、CC、CA为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C(0, 0, 0), B(4, 0, 0), B(4, －3, 0), C(0, －3, 0), A(0, 0, h), A(0, －3, h), G(2, －, －) ………………………  3分

=(2, －, －), =(0, －3, －h)  ……… 4分

·=0,  h=3

(2)设平面ABC得法向量=(a, b, c),则可求得=(3, 4, 0) (令a=3)

点A到平面ABC的距离为H=||=……… 8分

(3) 设平面ABC的法向量为=(x, y, z),则可求得=(0, 1, 1) (令z=1)

二面角C－AB－C的大小满足cos== ………  11分

二面角C－AB－C的平面角的正弦大小为

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网