题目内容
(13分)如图(2):PA⊥面ABCD,CD
2AB,
∠DAB=90°,E为PC的中点.
(1)证明:BE//面PAD;
(2)若PA=AD,证明:BE⊥面PDC.
(1)略 (2)略
解析:
(1)取PD的中点M,连ME,MA.
∵E为PC的中点 ∴ME
DC，又ABDC ∴ME
AB.即四边形ABEM为□，∴AM//BE且AM
面PAD ∴BE//面PAD.
(2) ∵PA=AD ∴AM⊥PD ①
由PA⊥面AC知:PA⊥DC，再由∠DAB=Rt∠，∴DC⊥面PAD ∴DC⊥AM ②
综合①与②知: AM⊥面PDC，由(1)AM//BE 故BE⊥面PDC.
练习册系列答案
阅读快车系列答案
相关题目
x(A>0, 
[0,4]的图象，且图象的最高点为
)；赛道的后一部分为折线段MNP，为保证参赛
MNP=120
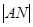长不超过
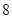米。
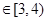（单位：米），则当AM、AN的长度是多少时，矩形花坛AMPN的面积最大？并求出最大面积．
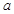,BD可长根据需要进行调节（BC足够长）。现规划在△ABD的内接正方形BEFG内种花，其余地方种草，且把种草的面积
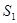与种花的面积
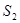的比值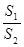
称为“草花比y”。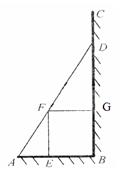
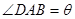，将
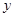表示成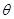
的函数关系式；
中，已知
侧面
（不包含端点
上确定一点
的位置，使得
(要求说明理由).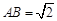
，求二面角
的大小.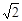
，E为DC中点，将它沿AE折成直二面角D-AE-B. 