Question

不等式（m²-2m-3）x²-(m-3)x-1<0对一切x∈R都成立.求实数m的取值范围.

Answer 1

思路分析：所给不等式不一定是二次的，当其是二次不等式时，结合相应图象，可得m应满足的不等式组，从而可求得m的取值范围.

解：令m²-2m-3=0，得m=3或-1.当m=3时，原不等式化为-1＜0,对一切x∈R，它都成立；当m=-1时，原不等式化为4x-1<0,它并非对一切x∈R成立.若m²-2m-3≠0,原不等式解集为R，需且只需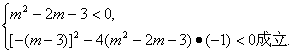

解这个不等式组得-＜m<3.

综合得m的取值范围是{m|-