题目内容
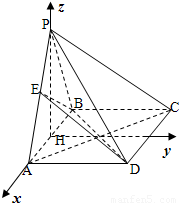
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,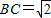 ,且侧面PAB是正三角形,平面PAB⊥平面ABCD.
,且侧面PAB是正三角形,平面PAB⊥平面ABCD.(1)求证:PD⊥AC;
(2)在棱PA上是否存在一点E,使得二面角E-BD-A的大小为45°,若存在,试求
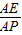 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.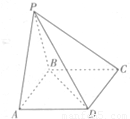
【答案】分析:(1)证明PH⊥平面ABCD,以H为原点,建立空间直角坐标系,用坐标表示向量,利用向量的数量积为0,即可证得结论;
(2)假设在棱PA上存在一点E,不妨设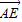 =λ
=λ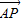 (0<λ<1),求得平面EBD的一个法向量、面ABD的法向量,利用向量的夹角公式,即可求得结论.
(0<λ<1),求得平面EBD的一个法向量、面ABD的法向量,利用向量的夹角公式,即可求得结论.
解答:(1)证明:取AB中点H,则由PA=PB,得PH⊥AB,又平面PAB⊥平面ABCD,且平面PAB∩平面ABCD=AB,所以PH⊥平面ABCD.以H为原点,建立空间直角坐标系H-xyz(如图).则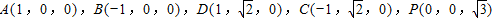 …..(2分)
…..(2分)
∵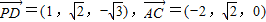 ,…..(4分)
,…..(4分)
∴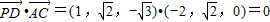 ,
,
∴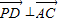 ,即PD⊥AC. …..(6分)
,即PD⊥AC. …..(6分)
(2)解:假设在棱PA上存在一点E,不妨设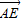 =λ
=λ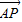 (0<λ<1),
(0<λ<1),
则点E的坐标为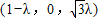 ,…..(8分)
,…..(8分)
∴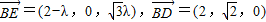
设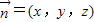 是平面EBD的法向量,则
是平面EBD的法向量,则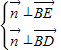 ,
,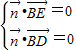
∴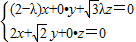
∴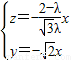 ,
,
不妨取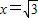 ,则得到平面EBD的一个法向量
,则得到平面EBD的一个法向量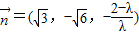 . …..(10分)
. …..(10分)
又面ABD的法向量可以是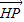 =(0,0,
=(0,0,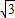 ),
),
要使二面角E-BD-A的大小等于45°,
则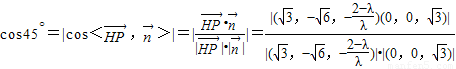
可解得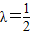 ,即
,即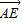 =
=
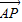
故在棱PA上存在点E,当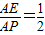 时,使得二面角E-BD-A的大小等于45°.…..(12分)
时,使得二面角E-BD-A的大小等于45°.…..(12分)
点评:本题考查线线垂直,考查面面角,考查利用向量法解决立体几何的能力,属于中档题.
(2)假设在棱PA上存在一点E,不妨设
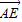 =λ
=λ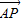 (0<λ<1),求得平面EBD的一个法向量、面ABD的法向量,利用向量的夹角公式,即可求得结论.
(0<λ<1),求得平面EBD的一个法向量、面ABD的法向量,利用向量的夹角公式,即可求得结论.解答:(1)证明:取AB中点H,则由PA=PB,得PH⊥AB,又平面PAB⊥平面ABCD,且平面PAB∩平面ABCD=AB,所以PH⊥平面ABCD.以H为原点,建立空间直角坐标系H-xyz(如图).则
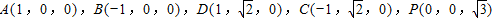 …..(2分)
…..(2分)∵
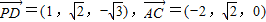 ,…..(4分)
,…..(4分)∴
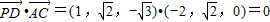 ,
,
∴
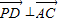 ,即PD⊥AC. …..(6分)
,即PD⊥AC. …..(6分)(2)解:假设在棱PA上存在一点E,不妨设
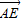 =λ
=λ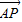 (0<λ<1),
(0<λ<1),则点E的坐标为
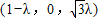 ,…..(8分)
,…..(8分)∴
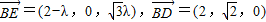
设
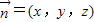 是平面EBD的法向量,则
是平面EBD的法向量,则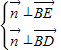 ,
,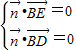
∴
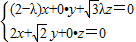
∴
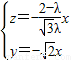 ,
,不妨取
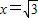 ,则得到平面EBD的一个法向量
,则得到平面EBD的一个法向量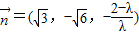 . …..(10分)
. …..(10分)又面ABD的法向量可以是
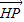 =(0,0,
=(0,0,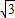 ),
),要使二面角E-BD-A的大小等于45°,
则
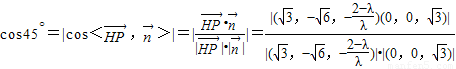
可解得
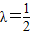 ,即
,即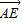 =
=
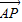
故在棱PA上存在点E,当
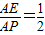 时,使得二面角E-BD-A的大小等于45°.…..(12分)
时,使得二面角E-BD-A的大小等于45°.…..(12分)点评:本题考查线线垂直,考查面面角,考查利用向量法解决立体几何的能力,属于中档题.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=