题目内容
下列命题中,真命题的是( )A.?φ∈R,函数y=sin(2x+φ)都不是偶函数
B.?x∈R,使得e2x+3ex+1=0
C.

D.“?x∈R,使2x>3”的否定是“?x∈R,使2x≤3”
【答案】分析:选项A,当φ=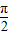 时,函数为偶函数;选项B,左边全为正数,不可能为0;选项C,当m=2时,符合题意;选项D,该命题的否定应该为“?x∈R,有2x≤3”,可得答案.
时,函数为偶函数;选项B,左边全为正数,不可能为0;选项C,当m=2时,符合题意;选项D,该命题的否定应该为“?x∈R,有2x≤3”,可得答案.
解答:解:选项A错误,当φ=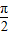 时,函数y=sin(2x+φ)=sin(2x+
时,函数y=sin(2x+φ)=sin(2x+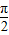 )=cosx为偶函数;
)=cosx为偶函数;
选项B错误,因为ex>0,e2x>0,左边全为正数,故不可能为0;
选项C正确,当m=2时,f(x)=x-1=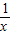 ,为幂函数,且在(0,+∞)上单调递减;
,为幂函数,且在(0,+∞)上单调递减;
选项D错误,该命题的否定应该为“?x∈R,有2x≤3”
故选C
点评:本题考查命题真假的判断,涉及函数的性质和特称命题的否定,属基础题.
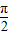 时,函数为偶函数;选项B,左边全为正数,不可能为0;选项C,当m=2时,符合题意;选项D,该命题的否定应该为“?x∈R,有2x≤3”,可得答案.
时,函数为偶函数;选项B,左边全为正数,不可能为0;选项C,当m=2时,符合题意;选项D,该命题的否定应该为“?x∈R,有2x≤3”,可得答案.解答:解:选项A错误,当φ=
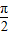 时,函数y=sin(2x+φ)=sin(2x+
时,函数y=sin(2x+φ)=sin(2x+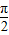 )=cosx为偶函数;
)=cosx为偶函数;选项B错误,因为ex>0,e2x>0,左边全为正数,故不可能为0;
选项C正确,当m=2时,f(x)=x-1=
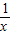 ,为幂函数,且在(0,+∞)上单调递减;
,为幂函数,且在(0,+∞)上单调递减;选项D错误,该命题的否定应该为“?x∈R,有2x≤3”
故选C
点评:本题考查命题真假的判断,涉及函数的性质和特称命题的否定,属基础题.

练习册系列答案
相关题目
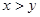 ,则
,则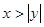 ”的逆命题
”的逆命题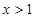 ,则
,则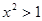 ”的否命题
”的否命题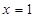 ,则
,则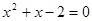 ”的否命题
”的否命题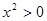 ,则
,则