题目内容
已知数列
为等差数列，公差
,且
（1）求证：当k取不同自然数时，此方程有公共根；
（2）若方程不同的根依次为
…,求证：数列
为等差数列.
（1）见解析；（2）见解析.
【解析】
试题分析：（1）依题意，
，于是原方程可转化为
，从而可证结论；（2）原方程另一根为
，利用韦达定理，可求得
,然后可得
；根据等差数列的定义，证明即可．
试题解析：（1）
是等差数列，
，
∴当k取不同自然数时，原方程有一个公共根-1．
（2）原方程另一根为
，则
,
,
,
∴数列
是以
为公差的等差数列.
考点：等差关系的确定；数列递推式．
练习册系列答案
相关题目
,
是椭圆的两个焦点，若椭圆上存在点P，使得
,则椭圆的离心率的取值范围是（ ）
B．
C．
D．
，则
的值为（ ）
，令点集
是
在D上取得最大值或最小值的点
，则
中的点最多能确定三角形的个数为（ ）某研究机构对儿童记忆能力
和识图能力
进行统计分析，得到如下数据：
记忆能力 | 4 | 6 | 8 | 10 |
识图能力 | 3 | 5 | 6 | 8 |
由表中数据，求得线性回归方程为
若某儿童的记忆能力为12时，则他的识图能力为( )
A.9.2 B.9.5 C.9.8 D.10
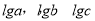成等差数列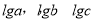 
成等比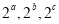数列 
成等差数列 
+z
=0”是“z1=z2=0”的 （ ）
B．
D．