题目内容
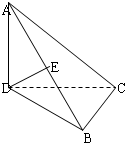 在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD.
在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD.
(Ⅰ)求证:DE⊥平面ABC;
(Ⅱ)求平面BAC与平面DAC夹角的余弦值.
(Ⅰ)证明:∵AD⊥平面BCD,BC?平面BCD
∴AD⊥BC
∵BD⊥BC,BD∩AD=D
∴BC⊥平面ABD
∵DE?平面ABD
∴DE⊥BC
∵DE⊥AB,AB∩BC=B
∴DE⊥平面ABC;
(Ⅱ)过点D作DF⊥AC,连接EF,则
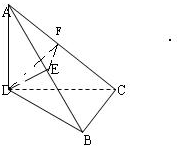
∵DE⊥平面ABC,
∴EF⊥AC
∴∠DFE为平面BAC与平面DAC夹角
在直角△ADC中,AD=2,DC= ,∴
,∴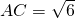 ,∵AD×DC=AC×DF,∴
,∵AD×DC=AC×DF,∴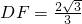
在直角△ADC中,AD=2,BD=1,∴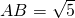 ,∵AD×DB=AB×DE,∴
,∵AD×DB=AB×DE,∴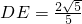
∴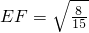
∴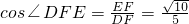
分析:(Ⅰ)证明DE⊥平面ABC,由于DE⊥AB,只需证明DE⊥BC,利用AD⊥平面BCD,BD⊥BC,可以证明BC⊥平面ABD,从而问题得证;
(Ⅱ)过点D作DF⊥AC,连接EF,根据DE⊥平面ABC,可知∠DFE为平面BAC与平面DAC夹角,分别计算出EF,DF的长,再利用余弦函数即可求得.
点评:本题以三棱锥为载体,考查线面垂直,解题的关键是正确理解与运用线面垂直的判定与性质,求面面角的关键是正确作出面面角
∴AD⊥BC
∵BD⊥BC,BD∩AD=D
∴BC⊥平面ABD
∵DE?平面ABD
∴DE⊥BC
∵DE⊥AB,AB∩BC=B
∴DE⊥平面ABC;
(Ⅱ)过点D作DF⊥AC,连接EF,则

∵DE⊥平面ABC,
∴EF⊥AC
∴∠DFE为平面BAC与平面DAC夹角
在直角△ADC中,AD=2,DC=
 ,∴
,∴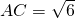 ,∵AD×DC=AC×DF,∴
,∵AD×DC=AC×DF,∴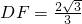
在直角△ADC中,AD=2,BD=1,∴
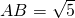 ,∵AD×DB=AB×DE,∴
,∵AD×DB=AB×DE,∴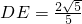
∴
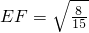
∴
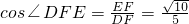
分析:(Ⅰ)证明DE⊥平面ABC,由于DE⊥AB,只需证明DE⊥BC,利用AD⊥平面BCD,BD⊥BC,可以证明BC⊥平面ABD,从而问题得证;
(Ⅱ)过点D作DF⊥AC,连接EF,根据DE⊥平面ABC,可知∠DFE为平面BAC与平面DAC夹角,分别计算出EF,DF的长,再利用余弦函数即可求得.
点评:本题以三棱锥为载体,考查线面垂直,解题的关键是正确理解与运用线面垂直的判定与性质,求面面角的关键是正确作出面面角

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( )
如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( ) 在三棱锥A-BCD中,AB=4,CD=2,且异面直线AB、CD所成的角为60°,若M、N分别是AD、BC的中点,则MN=
在三棱锥A-BCD中,AB=4,CD=2,且异面直线AB、CD所成的角为60°,若M、N分别是AD、BC的中点,则MN= (2011•渭南三模)在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD.
(2011•渭南三模)在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD. 如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜
如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜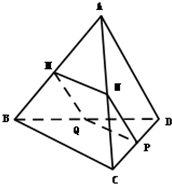 如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.
如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.