题目内容
(2011•顺义区二模)在复平面内,复数
对应的点的坐标为
| 1+2i |
| 1+i |
(
,
)
| 3 |
| 2 |
| 1 |
| 2 |
(
,
)
.| 3 |
| 2 |
| 1 |
| 2 |
分析:先把
等价转化为
,再由复数的运算法则得到
+
i.由此能求出复数
对应的点的坐标.
| 1+2i |
| 1+i |
| (1+2i)(1-i) |
| (1+i)(1-i) |
| 3 |
| 2 |
| 1 |
| 2 |
| 1+2i |
| 1+i |
解答:解:∵
=
=
=
+
i.
∴复数
对应的点的坐标为(
,
).
故答案为:(
,
).
| 1+2i |
| 1+i |
| (1+2i)(1-i) |
| (1+i)(1-i) |
=
| 3+i |
| 2 |
=
| 3 |
| 2 |
| 1 |
| 2 |
∴复数
| 1+2i |
| 1+i |
| 3 |
| 2 |
| 1 |
| 2 |
故答案为:(
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题考查复数的代数意义和几何表示,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
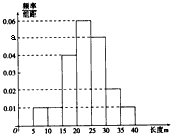 (2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=
(2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=