题目内容
一个口袋内有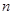 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是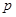 .
.
(I)当 时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数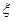 的期望
的期望 ;
;
(II)若 ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于 ,求
,求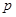 和
和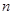 .
.
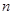 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是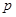 .
.(I)当
 时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数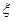 的期望
的期望 ;
;(II)若
 ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于 ,求
,求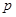 和
和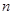 .
.(1)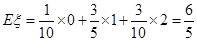 ;(2)
;(2)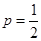 ,
,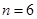 .
.
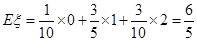 ;(2)
;(2)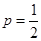 ,
,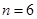 .
.本试题主要是考查了概率的求解和运算,利用古典概型,结合排列组合求解运算。同时也考查了分布列的求解,超几何分布列,期望公式的运用。
解:(I)法一: ,所以5个球中有2个白球
,所以5个球中有2个白球
白球的个数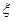 可取0,1,2.························· 1分
可取0,1,2.························· 1分
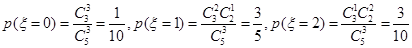 .······· 4分
.······· 4分
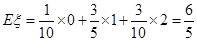 .······················· 6分
.······················· 6分
法二:白球个数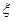 服从参数为
服从参数为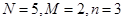 的超几何分布,则
的超几何分布,则 ……………………6分
……………………6分
(II)由题设知, ,···················· 8分
,···················· 8分
因为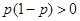 所以不等式可化为
所以不等式可化为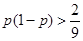 ,
,
解不等式得,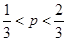 ,即
,即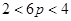 .·················· 10分
.·················· 10分
又因为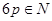 ,所以
,所以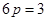 ,即
,即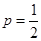 ,
,
所以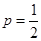 ,所以
,所以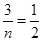 ,所以
,所以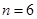 .···················· 12分
.···················· 12分
解:(I)法一:
 ,所以5个球中有2个白球
,所以5个球中有2个白球白球的个数
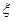 可取0,1,2.························· 1分
可取0,1,2.························· 1分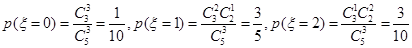 .······· 4分
.······· 4分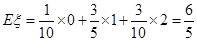 .······················· 6分
.······················· 6分法二:白球个数
 服从参数为
服从参数为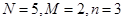 的超几何分布,则
的超几何分布,则 ……………………6分
……………………6分(II)由题设知,
 ,···················· 8分
,···················· 8分因为
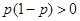 所以不等式可化为
所以不等式可化为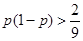 ,
,解不等式得,
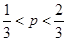 ,即
,即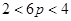 .·················· 10分
.·················· 10分又因为
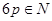 ,所以
,所以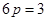 ,即
,即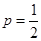 ,
,所以
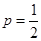 ,所以
,所以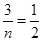 ,所以
,所以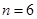 .···················· 12分
.···················· 12分
练习册系列答案
相关题目
 和
和 ,将
,将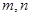 作为Q点的横、纵坐标,
作为Q点的横、纵坐标, 的夹角为
的夹角为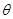 ,求
,求 的概率;
的概率; 内的概率.
内的概率. —
— ,且当二次方程
,且当二次方程 无实根时,
无实根时, ,则
,则 ( )
( ) 内随机地取出一个数
内随机地取出一个数 ,则
,则 的概率为 .
的概率为 .  、
、 ;不成功的概率依次为
;不成功的概率依次为 、
、 .
. ,求
,求 .
. 的概率为( )
的概率为( )







 人以上
人以上






