题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c.若sin Acos C+sin Ccos A=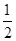 ,且a>b,则∠B等于 ( )
,且a>b,则∠B等于 ( )
A. | B. | C. | D. |
D
解析试题分析: ,因为
,因为 ,所以
,所以 为锐角,即
为锐角,即 。故D正确。
。故D正确。
考点:三角函数两角和差公式。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
已知 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
设△ABC的内角 所对的边分别为
所对的边分别为 ,若
,若 ,则
,则 的形状为( )
的形状为( )
| A.直角三角形 | B.锐角三角形 | C.钝角三角形 | D.不确定 |
若 ,且
,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
若 ,则
,则 的值为()
的值为()
A. | B. | C. | D. |
若 ,则
,则 ( )
( )
A. | B. | C. | D. |
若复数 是纯虚数,则
是纯虚数,则 的值为( )
的值为( )
| A.-7 | B. | C.7 | D. 或 或 |
已知 =5,则sin2α-sinαcosα的值是( )
=5,则sin2α-sinαcosα的值是( )
A. | B.- | C.-2 | D.2 |
已知函数 ,则
,则 是( )
是( )
A.最小正周期为 的奇函数 的奇函数 |
B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的偶函数 的偶函数 |