题目内容
随机变量ξ的分布列如下:其中a,2b,| 3 |
| 2 |
| 1 |
| 4 |
| ξ | -1 | 0 | 1 |
| P | a | b | c |
分析:由于对于随机变量ξ的分布列的图标可以知道:a+b+c=1,又中a,2b,
c成等差数列,可以得到:4b=a+
c,再有若Eξ=
,利用期望定义在列出a,b,c的方程解出,并代入方差的定义式即可.
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
解答:解:由题意可得:
⇒
,
所以该随机变量的分布列就具体,有方差的定义值:Dξ=(-1-
)2a+(0-
)2b+ (1-
)2c=(
)2×
+(
)2×
+(
)2×
=
.
故答案为:
|
|
所以该随机变量的分布列就具体,有方差的定义值:Dξ=(-1-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 11 |
| 16 |
故答案为:
| 11 |
| 16 |
点评:此题考查了随机变量分布列的性质,期望的定义,方差的定义,等差数列定义还考查了学生求解问题时方程的思想及学生求解时的计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知离散型随机变量X的分布列如表.若EX=0,DX=1,则a= ,b= .
| X | -1 | 0 | 1 | 2 | ||
| P | a | b | c |
|
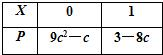 若离散型随机变量X的分布列如图,则常数c的值为( )
若离散型随机变量X的分布列如图,则常数c的值为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
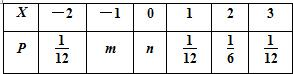 已知随机变量X的分布列如图:其中m,n∈[0,1),且E(X)=
已知随机变量X的分布列如图:其中m,n∈[0,1),且E(X)=| 1 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知离散型随机变量X 的分布列如右图.若E(X)=0,D(X)=1,则a、b、c的值依次为
已知离散型随机变量X 的分布列如右图.若E(X)=0,D(X)=1,则a、b、c的值依次为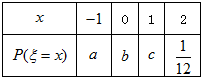 已知离散型随机变量x的分布列如右表.若Eξ=0,Dξ=1,则符合条件的一组数(a,b,c)=
已知离散型随机变量x的分布列如右表.若Eξ=0,Dξ=1,则符合条件的一组数(a,b,c)=