��Ŀ����
��p1��p2������pn��Ϊ����ʱ���� Ϊp1��p2������pn�ġ�������������֪����{an}�ĸ����Ϊ����������ǰn��ġ���������Ϊ
Ϊp1��p2������pn�ġ�������������֪����{an}�ĸ����Ϊ����������ǰn��ġ���������Ϊ ��
��
������������{an}��ͨ�ʽ��
������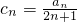 �����жϲ�˵��cn+1-cn��n��N*���ķ��ţ�
�����жϲ�˵��cn+1-cn��n��N*���ķ��ţ�
������֪ ��������{bn}��ǰn���ΪSn������
��������{bn}��ǰn���ΪSn������ ��ֵ��
��ֵ��
�������躯��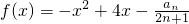 ���Ƿ��������ʵ���ˣ�ʹ��x�ܦ�ʱ������һ��������n������f��x����0�������
���Ƿ��������ʵ���ˣ�ʹ��x�ܦ�ʱ������һ��������n������f��x����0�������
�⣺��������ã�a1+a2++an-1+an=n��2n+1�� �٣�
a1+a2++an-1=��n-1����2n-1�� �ڣ�
��ʽ�������an=4n-1��n��2����
�� �����a1=3=4��1-1��
�����a1=3=4��1-1��
��an=4n-1��n��N+������4�֣�
����cn= ��cn+1=
��cn+1= ��
��
��cn+1-cn= ��0����cn+1��cn����7�֣�
��0����cn+1��cn����7�֣�
����bn=tan=t4n-1��t��0����
��Sn=b1+b2++bn=t3+t7++t4n-1��
��t=1ʱ��Sn=n�� ����8�֣�
����8�֣�
��t��0��t��1ʱ��Sn= ��
�� ����10�֣�
����10�֣�
���ϵã� ��11�֣�
��11�֣�
�������ɣ���֪����{cn}�ǵ����������У�c1=1�������С���cn��c1=1��
����������ʵ����ʹ��x�ܦ�ʱ������һ��������n������f��x��=-x2+4x- ��0�������
��0�������
��-x2+4x�� ��n��N+����
��n��N+����
ֻ��-x2+4x��c1=1����x2-4x+1��0��
��֮��x��2+ ��x��2-
��x��2- ��
��
���ǣ���ȡ��=2- ��14�֣�
��14�֣�
�����������������������a1+a2++an-1+an=n��2n+1����a1+a2++an-1=��n-1����2n-1������ʽ����Ϳ��������{an}��ͨ�ʽ��ע�����n=1�Ƿ��������
�������� ������õ�����{an}��ͨ�ʽ���뼴�����cn+1-cn�����ú����ĵ����ԾͿ��жϳ�cn+1-cn��n��N*���ķ��ţ�
�������� ������õ�����{an}��ͨ�ʽ���뼴���������{bn}��ͨ�ʽ���ٶԵȱ�����{bn}�ֹ��ȵ���1�Ͳ�����1��������ֱ���ͼ����ҵ� ��ֵ��
��ֵ��
�������ɣ���֪����{cn}�ǵ����������У�c1=1������С�����f��x����0���������ת��Ϊ-x2+4x��c1=1���ٽⲻ��ʽ�Ϳ��ҵ���Ӧ������ʵ���ˣ�
�����������Ƕ�����֪ʶ������֪ʶ�Լ������������ۺϿ��飮�����õȱ����е����ʽʱ��һ��Ҫ�����ȵ�ȡֵ���ڲ�ȷ��������£�Ҫ��������ۣ�
a1+a2++an-1=��n-1����2n-1�� �ڣ�
��ʽ�������an=4n-1��n��2����
��
 �����a1=3=4��1-1��
�����a1=3=4��1-1����an=4n-1��n��N+������4�֣�
����cn=
 ��cn+1=
��cn+1= ��
����cn+1-cn=
 ��0����cn+1��cn����7�֣�
��0����cn+1��cn����7�֣�����bn=tan=t4n-1��t��0����
��Sn=b1+b2++bn=t3+t7++t4n-1��
��t=1ʱ��Sn=n��
 ����8�֣�
����8�֣���t��0��t��1ʱ��Sn=
 ��
�� ����10�֣�
����10�֣����ϵã�
 ��11�֣�
��11�֣��������ɣ���֪����{cn}�ǵ����������У�c1=1�������С���cn��c1=1��
����������ʵ����ʹ��x�ܦ�ʱ������һ��������n������f��x��=-x2+4x-
 ��0�������
��0���������-x2+4x��
 ��n��N+����
��n��N+����ֻ��-x2+4x��c1=1����x2-4x+1��0��
��֮��x��2+
 ��x��2-
��x��2- ��
�����ǣ���ȡ��=2-
 ��14�֣�
��14�֣������������������������a1+a2++an-1+an=n��2n+1����a1+a2++an-1=��n-1����2n-1������ʽ����Ϳ��������{an}��ͨ�ʽ��ע�����n=1�Ƿ��������
�������� ������õ�����{an}��ͨ�ʽ���뼴�����cn+1-cn�����ú����ĵ����ԾͿ��жϳ�cn+1-cn��n��N*���ķ��ţ�
�������� ������õ�����{an}��ͨ�ʽ���뼴���������{bn}��ͨ�ʽ���ٶԵȱ�����{bn}�ֹ��ȵ���1�Ͳ�����1��������ֱ���ͼ����ҵ�
 ��ֵ��
��ֵ���������ɣ���֪����{cn}�ǵ����������У�c1=1������С�����f��x����0���������ת��Ϊ-x2+4x��c1=1���ٽⲻ��ʽ�Ϳ��ҵ���Ӧ������ʵ���ˣ�
�����������Ƕ�����֪ʶ������֪ʶ�Լ������������ۺϿ��飮�����õȱ����е����ʽʱ��һ��Ҫ�����ȵ�ȡֵ���ڲ�ȷ��������£�Ҫ��������ۣ�

��ϰ��ϵ�д�
�����Ŀ
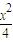 -
-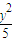 =1��x��2����O������ԭ�㣮
=1��x��2����O������ԭ�㣮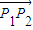 ���ɵı�Ϊ�ˣ��ˣ�0�������ˡ�[
���ɵı�Ϊ�ˣ��ˣ�0�������ˡ�[ ��
�� ]ʱ����|
]ʱ����|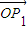 |•|
|•|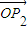 |����ֵ��
|����ֵ��