Question

（本小题满分12分）点A、B分别是椭圆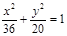长轴的左、右端点，点F是

 

椭圆的右焦点，点P在椭圆上，且位于轴上方，.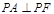

（1）求点P的坐标；

（2）设M是椭圆长轴AB上的一点，M到直线AP的距离等于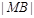，求椭圆上的点到点M的距离的最小值.

 

Answer 1

【答案】

解:（1）由已知可得点A(－6,0),F(0,4)   

设点P(,),则={+6, },={－4, },

由已知可得          则2+9－18=0, 解得=或=－6.

 

由于>0,只能=,于是=.    ∴点P的坐标是(,).…………………6分

 

（2）直线AP的方程是－+6=0.     设点M(,0),则M到直线AP的距离是.

 

于是=,又－6≤≤6,解得=2.  椭圆上的点(,)到点M的距离为,

 

则,

 

由于－6≤≤6, ∴当=时,取得最小值.………………………………12分

 

【解析】略