题目内容
已知函数f(x)是定义在R上的单调函数满足f(﹣3)=2,,且对任意的实数a∈R有f(﹣a)+f(a)=0恒成立.
(1)试判断f(x)在R上的单调性,并说明理由;
(2)解关于x的不等式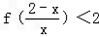 .
.
(1)试判断f(x)在R上的单调性,并说明理由;
(2)解关于x的不等式
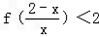 .
.解:(1)结论:f(x)是R上的减函数.理由如下
∵对任意的实数a∈R有f(﹣a)+f(a)=0
∴f(﹣a)=﹣f(a)对任意的实数a∈R成立,
可得函数f(x)是定义在R上的奇函数,
取x=0,得f(0)=0
∵f(x)在R上是单调函数,f(﹣3)=2>0=f(0)
∴f(x)为R上的减函数.
(2)由f(﹣3)=2,不等式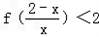 等价于
等价于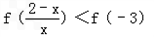
又∵f(x)为R上的减函数,
∴原不等式可化为: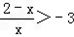
整理得: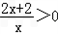 ,解之得:x<﹣1或x>0
,解之得:x<﹣1或x>0
∴不等式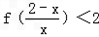 的解集为(﹣∞,﹣1)∪(0,+∞).
的解集为(﹣∞,﹣1)∪(0,+∞).
∵对任意的实数a∈R有f(﹣a)+f(a)=0
∴f(﹣a)=﹣f(a)对任意的实数a∈R成立,
可得函数f(x)是定义在R上的奇函数,
取x=0,得f(0)=0
∵f(x)在R上是单调函数,f(﹣3)=2>0=f(0)
∴f(x)为R上的减函数.
(2)由f(﹣3)=2,不等式
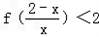 等价于
等价于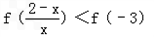
又∵f(x)为R上的减函数,
∴原不等式可化为:
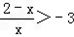
整理得:
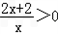 ,解之得:x<﹣1或x>0
,解之得:x<﹣1或x>0∴不等式
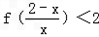 的解集为(﹣∞,﹣1)∪(0,+∞).
的解集为(﹣∞,﹣1)∪(0,+∞).
练习册系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+