题目内容
设双曲线 与直线l:x+y=1交于两个不同的点A,B,求双曲线C的离心率e的取值范围.
与直线l:x+y=1交于两个不同的点A,B,求双曲线C的离心率e的取值范围.
解:由C与l相交于两个不同的点,可知方程组 有两组不同的解,
有两组不同的解,
消去y,并整理得(1-a2)x2+2a2x-2a2=0,
∴ 解得
解得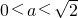 ,且a≠1,
,且a≠1,
而双曲线C的离心率e= ,从而
,从而 ,且
,且 ,
,
故双曲线C的离心率e的取值范围为
分析:由C与l相交于两个不同的点,可知方程组 有两组不同的解,确定a的范围,即可求得双曲线C的离心率e的取值范围.
有两组不同的解,确定a的范围,即可求得双曲线C的离心率e的取值范围.
点评:本题考查双曲线的性质,考查学生的计算能力,属于中档题.
 有两组不同的解,
有两组不同的解,消去y,并整理得(1-a2)x2+2a2x-2a2=0,
∴
 解得
解得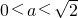 ,且a≠1,
,且a≠1,而双曲线C的离心率e=
 ,从而
,从而 ,且
,且 ,
,故双曲线C的离心率e的取值范围为

分析:由C与l相交于两个不同的点,可知方程组
 有两组不同的解,确定a的范围,即可求得双曲线C的离心率e的取值范围.
有两组不同的解,确定a的范围,即可求得双曲线C的离心率e的取值范围.点评:本题考查双曲线的性质,考查学生的计算能力,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
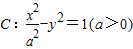 与直线l:x+y=1交于两个不同的点A,B,求双曲线C的离心率e的取值范围.
与直线l:x+y=1交于两个不同的点A,B,求双曲线C的离心率e的取值范围.