Question

对于函数y=f（x），x∈（0，+∞），如果a，b，c是一个三角形的三边长，那么f（a），f（b），f（c）也是一个三角形的三边长，则称函数f（x）为“保三角形函数”．
对于函数y=g（x），x∈[0，+∞），如果a，b，c是任意的非负实数，都有g（a），g（b），g（c）是一个三角形的三边长，则称函数g（x）为“恒三角形函数”．
（Ⅰ）判断三个函数“f₁（x）=x，f₂（x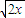）=，f₃（x）=3x²（定义域均为x∈（0，+∞））”中，哪些是“保三角形函数”？请说明理由；
（Ⅱ）若函数，x∈[{0，+∞}）是“恒三角形函数”，试求实数k的取值范围；
（Ⅲ）如果函数h（x）是定义在（0，+∞）上的周期函数，且值域也为（0，+∞），试证明：h（x）既不是“恒三角形函数”，也不是“保三角形函数”．

Answer 1

【答案】分析：（Ⅰ）不妨设a≤b≤c，由a+b＞c，能推出f₁（a）+f₁（b）＞c=f₁（c），可得f₁（x）是“保三角形函数”．
同理可得f₂（x）是“保三角形函数”．通过举反列a=3，b=3，c=5，f₃（a）+f₃（b）=f₃（c），
故f₃（x）不是“保三角形函数”．
（Ⅱ）当x=0时，g（x）=1；当x＞0时，，当k＞-1时，g（x）∈（1，k+2]，
由“恒三角形函数”的定义，1+1＞k+2，k＜0，故 有-1＜k＜0．
当k＜-1时，g（x）∈[k+2，1]，解 ，得，所以，．
将以上两个范围取并集．
（Ⅲ）因为存在正实数a，b，c，使得h（a）=1，h（b）=1，h（c）=2，故h（x）不是“恒三角形函数”．
由周期函数的定义，存在n＞m＞0，使得h（m）=1，h（n）=2，a，b，c是一个三角形的三边长，但因为
h（a）=h（b）=h（m）=1，h（c）=h（n）=2，故h（a），h（b），h（c）不是一个三角形的三边长，
h（x）也不是“保三角形函数”．
解答：解：（Ⅰ）对于f₁（x）=x，它在（0，+∞）上是增函数，
不妨设a≤b≤c，则f₁（a）≤f₁（b）≤f₁（c），因为a+b＞c，
所以f₁（a）+f₁（b）=a+b＞c=f₁（c），故f₁（x）是“保三角形函数”（2分）
对于，它在（0，+∞）上是增函数，
不妨设a≤b≤c，则f₂（a）≤f₂（b）≤f₂（c），因为a+b＞c，
所以=f₂（c），
故f₂（x）是“保三角形函数”（4分）
对于f₃（x）=3x²，取a=3，b=3，c=5，显然a，b，c是一个三角形的三边长，
但因为f₃（a）+f₃（b）=3×（3²+3²）＜3×5²=f₃（c），
所以，f₃（a）、f₃（b）、f₃（c）不是三角形的三边长，故f₃（x）不是“保三角形函数”（6分）
（Ⅱ）∵，
∴当x=0时，g（x）=1；  当x＞0时，．
当k＞-1时，因为，
所以，g（x）∈（1，k+2]，
从而当k＞-1时，g（x）∈[1，k+2]，由1+1＞k+2，得k＜0，所以，-1＜k＜0（9分）
当k＜-1时，因为，
所以，g（x）∈[k+2，1），
从而当k＜-1时，g（x）∈[k+2，1]，由，
得 ，所以，，
综上所述，所求k的取值范围是：．（11分）

（Ⅲ）①因为h（x）的值域为（0，+∞），∴存在正实数a，b，c，
使得h（a）=1，h（b）=1，h（c）=2，
显然这样的h（a），h（b），h（c）不是一个三角形的三边长，
故h（x）不是“恒三角形函数”（13分）
②因为h（x）是值域为（0，+∞）的周期函数，所以存在n＞m＞0，
使得h（m）=1，h（n）=2，
设h（x）的最小正周期为T（T＞0），
令a=b=m+kT，c=n，其中k∈N^*，且，
则a+b＞c，又显然b+c＞a，c+a＞b，所以a，b，c是一个三角形的三边长，
但因为h（a）=h（b）=h（m）=1，h（c）=h（n）=2，
所以h（a），h（b），h（c）不是一个三角形的三边长，
故h（x）也不是“保三角形函数”（16分）
点评：本题考查“保三角形函数”、“恒三角形函数”的定义，函数的单调性与周期性，体现了分类讨论的数学思想．