题目内容
已知f(x)= ,且方程f(x)=-4x+8有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn} 的前n项和分别为Sn,Tn且
,且方程f(x)=-4x+8有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn} 的前n项和分别为Sn,Tn且 (n∈N+).
(n∈N+).(1)若g(n)=
 ,求g(n)的最大值;
,求g(n)的最大值;(2)若a1=
 ,数列{bn}的公差为3,试问在数列{an} 与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由.
,数列{bn}的公差为3,试问在数列{an} 与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由.(3)若a1=
 ,数列{bn}的公差为3,且dn=bn-(n-1),h(x)=
,数列{bn}的公差为3,且dn=bn-(n-1),h(x)= .试证明:h(d1)•h(d2)…h(dn)<
.试证明:h(d1)•h(d2)…h(dn)< .
.
【答案】分析:(1)a=4时,f(x)= ,从而有:
,从而有: =f(n)=
=f(n)= ,g(n)=
,g(n)= =
= 结合函数的性质即可得出g(n)的最大值.
结合函数的性质即可得出g(n)的最大值.
(2)假若存在数列{an}中的第n项与数列{bn}中的第m项相等,即4n- =3m-2,进一步分析可得矛盾矛盾,即可得结论.
=3m-2,进一步分析可得矛盾矛盾,即可得结论.
(3)根据题意得h(dn)= ,要证h(d1)•h(d2)…h(dn)<
,要证h(d1)•h(d2)…h(dn)< 即要证
即要证 ×
× ×…×
×…× <
< (直接用数学归纳法证明不出)只要证明
(直接用数学归纳法证明不出)只要证明 ×
× ×…×
×…× <
< (再用数学归纳法证明即可).
(再用数学归纳法证明即可).
解答:解:(1)a=4,f(x)= ,
,
 =f(n)=
=f(n)=
g(n)= =
= ,
,
此函数是关于n的减函数,
当n=1时取得最大值,
故g(n)的最大值为g(1)= .
.
(2)由(1)知 ,
, 可得
可得
an=4n- ,bn=3n-2
,bn=3n-2
令an=bm,4n- =3m-2可得:
=3m-2可得: =3m-4n∈Z,矛盾
=3m-4n∈Z,矛盾
所以在数列{an} 与{bn}中不存在相等的项.
(3)证明:∵h(dn)=
∴要证h(d1)•h(d2)…h(dn)<
即要证 ×
× ×…×
×…× <
< (直接用数学归纳法证明不出)
(直接用数学归纳法证明不出)
只要证明 ×
× ×…×
×…× <
< (再用数学归纳法证明即可)
(再用数学归纳法证明即可)
①当n=1时, ×
× ×…×
×…× <
< 显然成立,当n=2时,
显然成立,当n=2时, ×
× ×…×
×…× <
< 成立;
成立;
②假设当n=k(k≥2)时 ×
× ×…×
×…× <
< 成立,
成立,
当n=k+1时,为了要证明: ×
× ×…×
×…× <
< 成立
成立
只要证:
?3(2k+1)2≤(3k+1)[(2k+2)2-(2k+1)2]=(3k+1)(4k+3)
?12k2+12k+3≤12k2+13k+3?k≥0.
最后一个式子显然成立,从而得出n=k+1时也成立.
由①②可得n∈N+时,h(d1)•h(d2)…h(dn)< .
.
点评:本题主要考查数学归纳法与等差数列的有关性质,以及等差数列的通项公式、函数求最值等知识点,属于中档题.
 ,从而有:
,从而有: =f(n)=
=f(n)= ,g(n)=
,g(n)= =
= 结合函数的性质即可得出g(n)的最大值.
结合函数的性质即可得出g(n)的最大值.(2)假若存在数列{an}中的第n项与数列{bn}中的第m项相等,即4n-
 =3m-2,进一步分析可得矛盾矛盾,即可得结论.
=3m-2,进一步分析可得矛盾矛盾,即可得结论.(3)根据题意得h(dn)=
 ,要证h(d1)•h(d2)…h(dn)<
,要证h(d1)•h(d2)…h(dn)< 即要证
即要证 ×
× ×…×
×…× <
< (直接用数学归纳法证明不出)只要证明
(直接用数学归纳法证明不出)只要证明 ×
× ×…×
×…× <
< (再用数学归纳法证明即可).
(再用数学归纳法证明即可).解答:解:(1)a=4,f(x)=
 ,
, =f(n)=
=f(n)=
g(n)=
 =
= ,
,此函数是关于n的减函数,
当n=1时取得最大值,
故g(n)的最大值为g(1)=
 .
.(2)由(1)知
 ,
, 可得
可得an=4n-
 ,bn=3n-2
,bn=3n-2令an=bm,4n-
 =3m-2可得:
=3m-2可得: =3m-4n∈Z,矛盾
=3m-4n∈Z,矛盾所以在数列{an} 与{bn}中不存在相等的项.
(3)证明:∵h(dn)=

∴要证h(d1)•h(d2)…h(dn)<

即要证
 ×
× ×…×
×…× <
< (直接用数学归纳法证明不出)
(直接用数学归纳法证明不出)只要证明
 ×
× ×…×
×…× <
< (再用数学归纳法证明即可)
(再用数学归纳法证明即可)①当n=1时,
 ×
× ×…×
×…× <
< 显然成立,当n=2时,
显然成立,当n=2时, ×
× ×…×
×…× <
< 成立;
成立;②假设当n=k(k≥2)时
 ×
× ×…×
×…× <
< 成立,
成立,当n=k+1时,为了要证明:
 ×
× ×…×
×…× <
< 成立
成立只要证:

?3(2k+1)2≤(3k+1)[(2k+2)2-(2k+1)2]=(3k+1)(4k+3)
?12k2+12k+3≤12k2+13k+3?k≥0.
最后一个式子显然成立,从而得出n=k+1时也成立.
由①②可得n∈N+时,h(d1)•h(d2)…h(dn)<
 .
.点评:本题主要考查数学归纳法与等差数列的有关性质,以及等差数列的通项公式、函数求最值等知识点,属于中档题.

练习册系列答案
相关题目
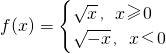 且f(a)+f(4)=4,那么a=-4;
且f(a)+f(4)=4,那么a=-4;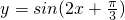 的图象,只要将y=sin2x的图象向左平移
的图象,只要将y=sin2x的图象向左平移 单位;
单位;