题目内容
 如图,圆O的两条弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G,EF=2,则FG的长为( )
如图,圆O的两条弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G,EF=2,则FG的长为( )分析:根据平行线的性质,得到∠DEF=∠C.由圆周角定理得到∠A=∠C,从而∠DEF=∠A,由此可得△DFE∽△EFA,利用对应边成比例证出EF2=FD•FA,最后根据切割线定理证出FG2=FD•FA,得EF=FG=2,从而得到答案.
解答:解:∵EF∥CB,∴∠DEF=∠C.
∵圆O中,∠A、∠C同对弧BD,∴∠A=∠C.
因此∠DEF=∠A,
∵∠DFE=∠EFA,∴△DFE∽△EFA,得
=
∴EF2=FD•FA,
∵FG切圆O于点G,∴FG2=FD•FA,可得EF=FG
∵EF=2,∴FG的长为2.
故选:D
∵圆O中,∠A、∠C同对弧BD,∴∠A=∠C.
因此∠DEF=∠A,
∵∠DFE=∠EFA,∴△DFE∽△EFA,得
| FD |
| EF |
| EF |
| FA |
∴EF2=FD•FA,
∵FG切圆O于点G,∴FG2=FD•FA,可得EF=FG
∵EF=2,∴FG的长为2.
故选:D
点评:本题给出圆的切线和弦的平行线,求证三角形相似并求线段的长.着重考查了相似三角形的判定与性质、圆周角定理和切割线定理等知识,属于中档题.

练习册系列答案
相关题目
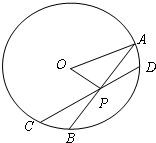 如图,AB,CD是半径为a的圆O的两条弦,他们相交于AB的中点P,PD=
如图,AB,CD是半径为a的圆O的两条弦,他们相交于AB的中点P,PD= (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. (1)不等式|2x-1|-|x+2|≥1的解集
(1)不等式|2x-1|-|x+2|≥1的解集 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)