题目内容
已知数列{an}的前n项和为Sn,a1=1,且nan+1=2Sn,数列{bn}满足b1= ,b2=
,b2= ,对任意n∈N*.都有
,对任意n∈N*.都有 =bn•bn+2.
=bn•bn+2.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)令Tn=a1b1+a2b2+…+anbn,若对任意的n∈N*,不等式λnTn+2bnSn<2(λn+3bn)恒成立,试求实数λ的取值范围.
解:(Ⅰ)∵nan+1=2Sn,∴(n-1)an=2Sn-1(n≥2),两式相减得,nan+1-(n-1)an=2an,
∴nan+1=(n+1)an=,即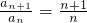 ,
,
∴an= =n(n≥2),
=n(n≥2),
a1=1满足上式,故数列{an}的通项公式an=n(n∈N*).
在数列{bn}中,由 =bn•bn+2,b1=
=bn•bn+2,b1= ,b2=
,b2= ,知数列{bn}是等比数列,首项、公比均为
,知数列{bn}是等比数列,首项、公比均为 ,
,
∴数列{bn}的通项公式bn= ;
;
(Ⅱ)∵Tn=a1b1+a2b2+…+anbn= +2×
+2× +…+n×
+…+n× ①
①
∴ Tn=
Tn= +2×
+2× +…+(n-1)×
+…+(n-1)× +
+ ②
②
由①-②,得 Tn=
Tn= +
+ +
+ +…+
+…+ -
- =1-
=1- ,
,
∴Tn=2-
∴不等式λnTn+2bnSn<2(λn+3bn)即为λn(2- )+
)+ <2(λn+
<2(λn+ ),
),
即(1-λ)n2+(1-2λ)n-6<0恒成立.
设f(n)=(1-λ)n2+(1-2λ)n-6,
当λ=1时,f(n)=-n-6<0成立,则λ=1满足条件;
当λ<1时,由二次函数性质知不恒成立;
当λ>1时,由于 <0,则f(n)在[1,+∞)上单调递减,f(n)≤f(1)=-3λ-4<0恒成立,则λ>1满足条件.
<0,则f(n)在[1,+∞)上单调递减,f(n)≤f(1)=-3λ-4<0恒成立,则λ>1满足条件.
综上所述,实数λ的取值范围是[1,+∞).
分析:(Ⅰ)利用nan+1=2Sn,再写一式,两式相减,再叠乘,即可求数列{an}的通项公式;在数列{bn}中,由 =bn•bn+2,b1=
=bn•bn+2,b1= ,b2=
,b2= ,知数列{bn}是等比数列,首项、公比均为
,知数列{bn}是等比数列,首项、公比均为 ,由此可得数列{bn}的通项公式;
,由此可得数列{bn}的通项公式;
(Ⅱ)利用错位相减法求数列的和,再将不等式转化为(1-λ)n2+(1-2λ)n-6<0恒成立,构造函数,利用函数的性质,即可确定实数λ的取值范围.
点评:本题考查数列递推式,考查数列的通项,考查错位相减法求数列的和,考查恒成立问题,确定数列的通项,正确求和是关键.
∴nan+1=(n+1)an=,即
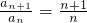 ,
,∴an=
 =n(n≥2),
=n(n≥2),a1=1满足上式,故数列{an}的通项公式an=n(n∈N*).
在数列{bn}中,由
 =bn•bn+2,b1=
=bn•bn+2,b1= ,b2=
,b2= ,知数列{bn}是等比数列,首项、公比均为
,知数列{bn}是等比数列,首项、公比均为 ,
,∴数列{bn}的通项公式bn=
 ;
;(Ⅱ)∵Tn=a1b1+a2b2+…+anbn=
 +2×
+2× +…+n×
+…+n× ①
①∴
 Tn=
Tn= +2×
+2× +…+(n-1)×
+…+(n-1)× +
+ ②
②由①-②,得
 Tn=
Tn= +
+ +
+ +…+
+…+ -
- =1-
=1- ,
,∴Tn=2-

∴不等式λnTn+2bnSn<2(λn+3bn)即为λn(2-
 )+
)+ <2(λn+
<2(λn+ ),
),即(1-λ)n2+(1-2λ)n-6<0恒成立.
设f(n)=(1-λ)n2+(1-2λ)n-6,
当λ=1时,f(n)=-n-6<0成立,则λ=1满足条件;
当λ<1时,由二次函数性质知不恒成立;
当λ>1时,由于
 <0,则f(n)在[1,+∞)上单调递减,f(n)≤f(1)=-3λ-4<0恒成立,则λ>1满足条件.
<0,则f(n)在[1,+∞)上单调递减,f(n)≤f(1)=-3λ-4<0恒成立,则λ>1满足条件.综上所述,实数λ的取值范围是[1,+∞).
分析:(Ⅰ)利用nan+1=2Sn,再写一式,两式相减,再叠乘,即可求数列{an}的通项公式;在数列{bn}中,由
 =bn•bn+2,b1=
=bn•bn+2,b1= ,b2=
,b2= ,知数列{bn}是等比数列,首项、公比均为
,知数列{bn}是等比数列,首项、公比均为 ,由此可得数列{bn}的通项公式;
,由此可得数列{bn}的通项公式;(Ⅱ)利用错位相减法求数列的和,再将不等式转化为(1-λ)n2+(1-2λ)n-6<0恒成立,构造函数,利用函数的性质,即可确定实数λ的取值范围.
点评:本题考查数列递推式,考查数列的通项,考查错位相减法求数列的和,考查恒成立问题,确定数列的通项,正确求和是关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |