题目内容
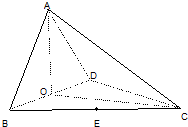 如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=| 2 |
(1)求证:AO⊥平面BCD;
(2)求几何体E-ACD的体积.
分析:(1)连接OC,由等腰三角形三线合一,可得AO⊥BD,CO⊥BD,再勾股定理可得AO⊥OC,进而根据线面垂直的判定定理得到AO⊥平面BCD;
(2)根据等积法可得VE-ACD=VA-CDE,结合(1)中结论,可得AO即为棱锥的高,代入棱锥的体积公式,可得答案.
(2)根据等积法可得VE-ACD=VA-CDE,结合(1)中结论,可得AO即为棱锥的高,代入棱锥的体积公式,可得答案.
解答: 证明:(1)连接OC
证明:(1)连接OC
∵BO=DO,AB=AD,
∴AO⊥BD.…(2分)
∵BO=DO,BC=CD,
∴CO⊥BD.
在△AOC中,由已知可得AO=1,CO=
.而AC=2,
∴AO2+CO2=AC2,
∴∠AOC=90°,
即AO⊥OC.…(5分)
又AO⊥BD,BD∩OC=O,BD,OC?平面BCD
∴AO⊥平面BCD…(7分)
解:(2)∵VE-ACD=VA-CDE,
在△ACD中,CA=CD=2,AD=
,
而AO=1,S△CDE=
×
×22=
,…(12分)
∴VE-ACD=VA-ECD=
AO.S△CDE═
.…(14分)
 证明:(1)连接OC
证明:(1)连接OC∵BO=DO,AB=AD,
∴AO⊥BD.…(2分)
∵BO=DO,BC=CD,
∴CO⊥BD.
在△AOC中,由已知可得AO=1,CO=
| 3 |
∴AO2+CO2=AC2,
∴∠AOC=90°,
即AO⊥OC.…(5分)
又AO⊥BD,BD∩OC=O,BD,OC?平面BCD
∴AO⊥平面BCD…(7分)
解:(2)∵VE-ACD=VA-CDE,
在△ACD中,CA=CD=2,AD=
| 2 |
而AO=1,S△CDE=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
∴VE-ACD=VA-ECD=
| 1 |
| 3 |
| ||
| 6 |
点评:本题考查的知识点是直线与平面垂直的判定,棱锥的体积公式,熟练掌握空间直线与直线垂直与直线与平面垂直相互之间的转化关系是解答的关键.

练习册系列答案
相关题目
 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形, 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD= 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.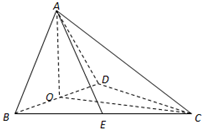 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.