题目内容
已知数列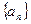 满足
满足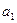 =-1,
=-1,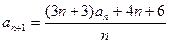 ,数列
,数列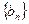 满足
满足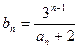
(1)求数列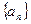 的通项公式.
的通项公式.
(2)设数列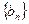 的前
的前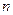 项和为
项和为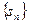 ,求证:当
,求证:当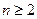 时,
时,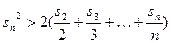 .
.
(3)求证:当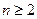 时,
时,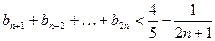
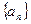 满足
满足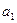 =-1,
=-1,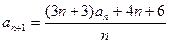 ,数列
,数列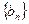 满足
满足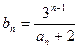
(1)求数列
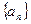 的通项公式.
的通项公式.(2)设数列
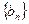 的前
的前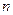 项和为
项和为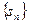 ,求证:当
,求证:当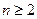 时,
时,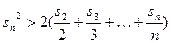 .
.(3)求证:当
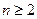 时,
时,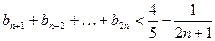
(1)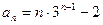 .
.
(2)证明略.
(3)证明略
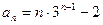 .
.(2)证明略.
(3)证明略
(1)由题意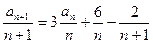 ,即
,即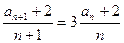
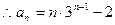 ………………………………4分
………………………………4分
(2)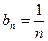 当
当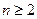 时,
时,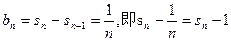
平方则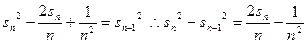
叠加得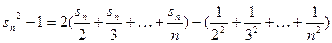
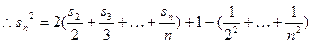
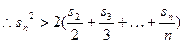 ……………………………………8分
……………………………………8分
(3)当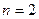 时,
时,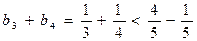 即
即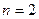 时命题成立
时命题成立
假设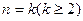 时命题成立,即
时命题成立,即
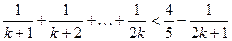
当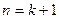 时,
时,
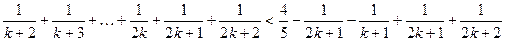
=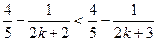
 即
即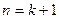 时命题也成立
时命题也成立
综上,对于任意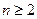 ,
,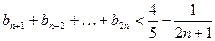 ………………12分
………………12分
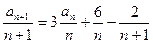 ,即
,即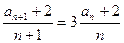
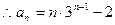 ………………………………4分
………………………………4分(2)
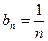 当
当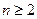 时,
时,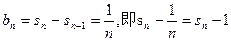
平方则
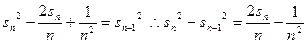
叠加得
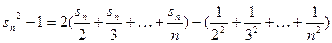
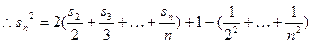
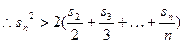 ……………………………………8分
……………………………………8分(3)当
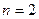 时,
时,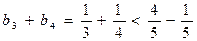 即
即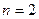 时命题成立
时命题成立假设
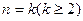 时命题成立,即
时命题成立,即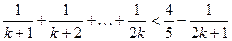
当
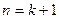 时,
时,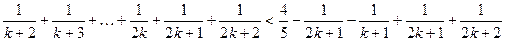
=
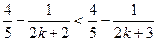
 即
即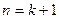 时命题也成立
时命题也成立综上,对于任意
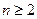 ,
,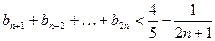 ………………12分
………………12分
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
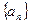 中,已知
中,已知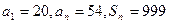 ,求
,求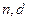 。
。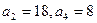 ,求
,求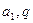 。
。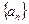 其前
其前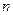 项和
项和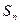 ,满足
,满足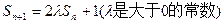 ,且
,且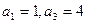 。
。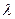 的值;
的值;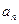 ;
;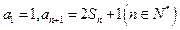
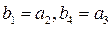 ,求数列
,求数列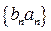 的前n项和为Tn(8分)
的前n项和为Tn(8分) 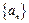 是等差数列,
是等差数列,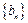 是等比数列,且
是等比数列,且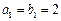 ,
,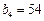 ,
,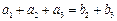 .
.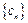 满足
满足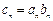 ,求数列
,求数列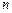 项和
项和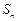 .
.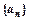 是公比为q的等比数列,且
是公比为q的等比数列,且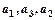 成等差数列,则q="( " )
成等差数列,则q="( " )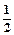
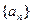 中,
中,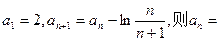 ( )
( )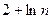
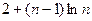
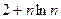
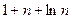
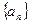 的通项公式
的通项公式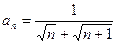 ,则该数列的前( )项之和等于
,则该数列的前( )项之和等于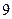 。
。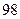
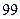
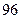
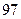
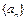 中,前n项和
中,前n项和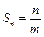 ,前m项和
,前m项和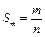 ,其中
,其中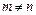 ,则
,则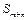 的值( )
的值( )