题目内容
(12分)已知直线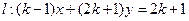 和圆
和圆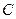 :
: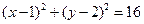 .
.
①求证:无论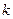 取何值,直线
取何值,直线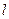 与圆
与圆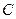 都相交;
都相交;
②求直线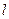 被圆
被圆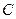 截得的弦长的最小值和弦长取得最小值时实数
截得的弦长的最小值和弦长取得最小值时实数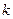 的值.
的值.
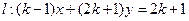 和圆
和圆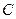 :
: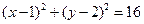 .
.①求证:无论
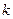 取何值,直线
取何值,直线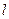 与圆
与圆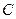 都相交;
都相交; ②求直线
 被圆
被圆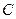 截得的弦长的最小值和弦长取得最小值时实数
截得的弦长的最小值和弦长取得最小值时实数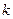 的值.
的值.解:①因为直线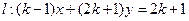 ,即
,即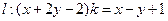 ,
,
由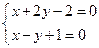 得
得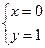 ,所以直线
,所以直线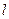 恒过定点
恒过定点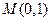 .-----------------3分
.-----------------3分
又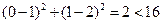 ,则点
,则点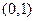 在圆
在圆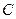 的内部,所以无论
的内部,所以无论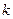 取何值,直线
取何值,直线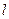 与圆
与圆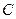 都相交.----------------------------------------------------------------------5分
都相交.----------------------------------------------------------------------5分
②设直线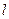 与圆
与圆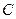 相交于
相交于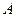 、
、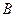 两点,圆心
两点,圆心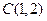 到直线
到直线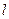 的距离为
的距离为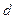 ,圆
,圆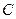 的半径为
的半径为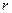 ,则
,则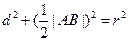 ,要使
,要使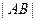 最小,当
最小,当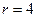 时,只需要
时,只需要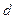 最大即可.又因为
最大即可.又因为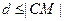 ,所以当
,所以当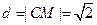 时,
时,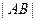 最小. ----------------8分
最小. ----------------8分
此时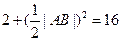 ,所以
,所以 .-----------------------------------9分
.-----------------------------------9分
当弦长 时,直线
时,直线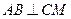 .
.
又因为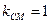 ,所以直线
,所以直线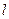 的斜率
的斜率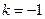 .---------------------------------11分
.---------------------------------11分
又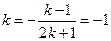 ,所以
,所以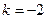 .-------------------------------------------12分
.-------------------------------------------12分
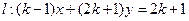 ,即
,即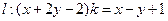 ,
,由
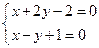 得
得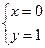 ,所以直线
,所以直线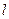 恒过定点
恒过定点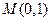 .-----------------3分
.-----------------3分又
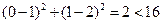 ,则点
,则点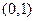 在圆
在圆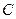 的内部,所以无论
的内部,所以无论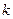 取何值,直线
取何值,直线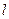 与圆
与圆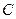 都相交.----------------------------------------------------------------------5分
都相交.----------------------------------------------------------------------5分②设直线
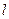 与圆
与圆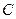 相交于
相交于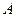 、
、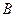 两点,圆心
两点,圆心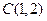 到直线
到直线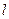 的距离为
的距离为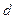 ,圆
,圆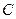 的半径为
的半径为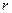 ,则
,则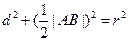 ,要使
,要使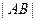 最小,当
最小,当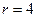 时,只需要
时,只需要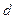 最大即可.又因为
最大即可.又因为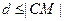 ,所以当
,所以当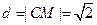 时,
时,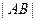 最小. ----------------8分
最小. ----------------8分此时
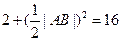 ,所以
,所以 .-----------------------------------9分
.-----------------------------------9分当弦长
 时,直线
时,直线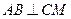 .
.又因为
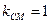 ,所以直线
,所以直线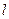 的斜率
的斜率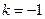 .---------------------------------11分
.---------------------------------11分又
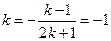 ,所以
,所以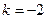 .-------------------------------------------12分
.-------------------------------------------12分略

练习册系列答案
相关题目
 的圆心坐标和半径分别为( )
的圆心坐标和半径分别为( )



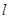 与圆
与圆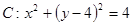 有公共点, 则直线
有公共点, 则直线
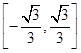
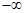 ,
,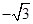 )∪[
)∪[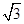 ,+
,+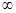 ]
]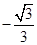 )∪[
)∪[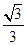 ,+
,+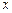 轴相切,圆心在直线
轴相切,圆心在直线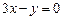 上,且被直线
上,且被直线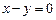 截下的弦长为
截下的弦长为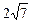 的圆的方程。
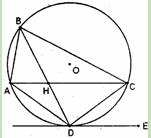
的圆的方程。 是圆
是圆 的直径,
的直径, 、
、 是圆上的点,
是圆上的点, ,弧
,弧 和弧
和弧 的长相等,
的长相等, 是圆
是圆





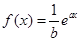 的图象在
的图象在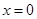 处的切线
处的切线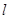 与圆
与圆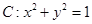 相离,则
相离,则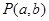 与圆C的位置关系是
与圆C的位置关系是 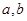 的取值有关
的取值有关 ≤λ≤1
≤λ≤1  <
<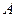 、
、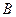 、
、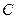 、
、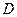 为圆
为圆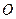 上的四点,直线
上的四点,直线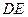 为圆
为圆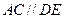 ,
,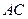 与
与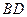 相交于
相交于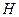 点 ⑴ 求证:
点 ⑴ 求证: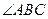 ⑵
⑵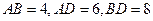 ,求
,求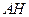 的长.
的长.