题目内容
 在可行域内任取一点,规则如图所示,则能输出数对(x,y)的概率为
在可行域内任取一点,规则如图所示,则能输出数对(x,y)的概率为| π |
| 16 |
| π |
| 16 |
分析:输入框中的可行域是用含绝对值的不等式表示的,我们可以通过分段找出对应的不等式组,通过作图找出四个不等式组表示的平面区域,再找出其中能输出数对(x,y)的平面区域,然后分别求出面积,则概率可求.
解答:解:由|x|+|y-
|≤
得
或
或
或
以上四个不等式组表示的平面区域为以(0,0)、(
,
)、(0,2
)、(-
,
)为顶点的正方形区域,而其中满足x2+y2≤1的有序数对(x,y)表示的区域为四分之一圆周,所以能输出数对(x,y)的概率为四分之一圆周的面积比上正方形的面积,结果为
=
,

故答案为
.
| 2 |
| 2 |
|
|
|
|
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 4 |
| π |
| 16 |

故答案为
| π |
| 16 |
点评:本题考查的是程序框图,同时重点考查了几何概型,解答该题的关键是把含绝对值的不等式转化为不等式组,注意测度比是面积比,解题过程运用了数学转化思想.

练习册系列答案
相关题目
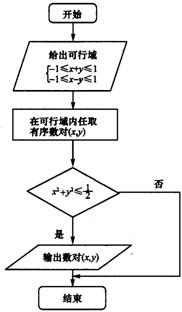 在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是( )
在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
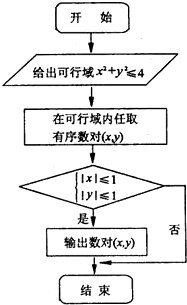 在可行域内任取一点,规则如流程图所示,则能输出数对(x,y)的概率是
在可行域内任取一点,规则如流程图所示,则能输出数对(x,y)的概率是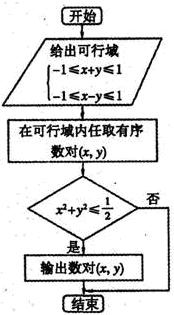 在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是
在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是 在可行域内任取一点,规则如程序框图所示,求能输出数对(x,y)的概率.
在可行域内任取一点,规则如程序框图所示,求能输出数对(x,y)的概率. (2012•许昌三模)在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是( )
(2012•许昌三模)在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是( )