题目内容
已知点 ,点
,点 为直线
为直线 上的一个动点.
上的一个动点.
(Ⅰ)求证: 恒为锐角;
恒为锐角;
(Ⅱ)若四边形 为菱形,求
为菱形,求 的值.
的值.
【答案】
(Ⅰ)证明见解析;(Ⅱ)2.
【解析】
试题分析:(Ⅰ)已知一个角的两边的向量,可以求出这个角的大小,由题,可以求出向量PA,PB,由向量内积公式可求得角的范围;(Ⅱ)菱形的对边平行且四边相等,向量相等,横纵坐标相等,由题,向量AP=BP,可以求得x=1,由向量PQ=BA,可以求得Q点坐标,即可求出向量的内积.
试题解析:(Ⅰ)∵点 在直线
在直线 上,
上,
∴点 ,
,
∴ ,
,
∴ ,
,
∴ ,
,
若 三点在一条直线上,则
三点在一条直线上,则 ,
,
得到 ,方程无解,
,方程无解,
∴ ,
,
∴ 恒为锐角.
恒为锐角.
(Ⅱ)∵四边形 为菱形,
为菱形,
∴ ,即
,即
化简得到 ,
,
∴ ,
,
∴ ,
,
设 ,∵
,∵ ,
,
∴ ,
,
∴ ,
,
∴ .
.
考点:1.用向量的内积求角;2.菱形.

练习册系列答案
相关题目
 ,点
,点 在直线
在直线 上运动,过点
上运动,过点 垂直的直线和
垂直的直线和 的中垂线相交于点
的中垂线相交于点 .
. 的方程;
的方程; 是轨迹
是轨迹 ,
, 在
在 轴上,圆
轴上,圆
 (
( 为参数)内切于
为参数)内切于 ,求
,求 ,点
,点 在直线
在直线 上运动,过点
上运动,过点 垂直的直线和
垂直的直线和 的中垂线相交于点
的中垂线相交于点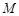 .
. 的方程;
的方程; 是轨迹
是轨迹 ,
, 在
在 轴上,圆
轴上,圆
 (
( 为参数)内切于
为参数)内切于 ,求
,求