Question

已知函数f(x)=x⁴+bx³+cx²+dx+e(x∈R)分别在x=0处和x=1处取得极值.

(1)求d的值及b与c的关系式(用c表示b),并指出c的取值范围;

(2)若函数f(x)在x=0处取得极大值,

①判断c的取值范围;

②若此时函数f(x)在x=1时取得最小值,求c的取值范围.

Answer 1

解:(1)∵f′(x)=2x³+3bx²+2cx+d,

又∵f′(0)=f′(1)=0,∴∴

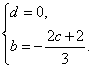
∵f′(x)=2x³-2(c+1)x²+2cx,即f′(x)=2x(x-1)(x-c),

∴c≠0且c≠1,

即c的取值范围是{c|c∈R且c≠0且c≠1}.

(2)①∵f′(x)=2x(x-1)(x-c),

∴当c＜0时,有

x	(-∞,c)	c	(c,0)	0	(0,1)	1	(1,+∞)
f′(x)	-	0	+	0	-	0	+
f(x)	递减	极小值	递增	极大值	递减	极小值	递增

符合题意.

当0＜c＜1或c＞1时,不符合题意.

即c的取值范围是{c|c＜0}.

②由题意得:f(c)≥f(1).

∴c⁴+c³+e≥+c+e.

∴c⁴-2c³+2c-1≤0,即(c-1)³(c+1)≤0.

∴-1≤c＜0,

即:c的取值范围是{c|-1≤c＜0}.