题目内容
设函数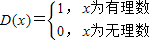
，则下列结论错误的是（ ）A．D（x）的值域为{0，1}
B．D（x）是偶函数
C．D（x）不是周期函数
D．D（x）不是单调函数
【答案】分析：由函数值域的定义易知A结论正确；由函数单调性定义，易知D结论正确；由偶函数定义可证明B结论正确；由函数周期性定义可判断D结论错误，故选C
解答：解：A显然正确；
∵
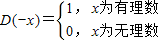=D（x），∴D（x）是偶函数，B正确；
∵D（x+1）=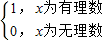
=D（x），∴T=1为其一个周期，故C错误；
∵D（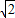
）=0，D（2）=1，D（
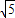）=0，显然函数D（x）不是单调函数，D正确；
故选 C
点评：本题主要考查了函数的定义，偶函数的定义和判断方法，函数周期性的定义和判断方法，函数单调性的意义，属基础题
解答：解：A显然正确；
∵
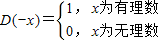=D（x），∴D（x）是偶函数，B正确；∵D（x+1）=
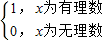=D（x），∴T=1为其一个周期，故C错误；∵D（
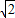）=0，D（2）=1，D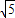（）=0，显然函数D（x）不是单调函数，D正确；故选 C
点评：本题主要考查了函数的定义，偶函数的定义和判断方法，函数周期性的定义和判断方法，函数单调性的意义，属基础题
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目