题目内容
若 是空间中互不相同的直线,
是空间中互不相同的直线, 是不重合的两平面,则下列命题中为真命题的是( )
是不重合的两平面,则下列命题中为真命题的是( )
 是空间中互不相同的直线,
是空间中互不相同的直线, 是不重合的两平面,则下列命题中为真命题的是( )
是不重合的两平面,则下列命题中为真命题的是( )A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则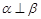 |
D
试题分析:选项A中,
 除平行n外,还有异面的位置关系,则A不正确.
除平行n外,还有异面的位置关系,则A不正确.选项B中,
 与β的位置关系有相交、平行、在β内三种,则B不正确.
与β的位置关系有相交、平行、在β内三种,则B不正确.选项C中,
 与m的位置关系还有相交和异面,故C不正确.
与m的位置关系还有相交和异面,故C不正确.选项D中,由
 ∥β,设经过
∥β,设经过 的平面与β相交,交线为c,则
的平面与β相交,交线为c,则 ∥c,又
∥c,又 ⊥α,故c⊥α,又c?β,所以
⊥α,故c⊥α,又c?β,所以 ⊥β,正确.
⊥β,正确.故选D.
点评:本题考查空间直线位置关系问题及判定,及面面垂直、平行的判定与性质,要综合判定定理与性质定理解决问题.

练习册系列答案
相关题目
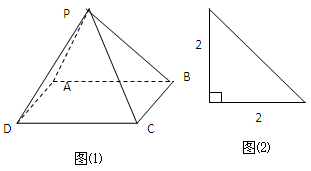

 ABC的边AB,BC,CA的中点,O是△ABC的重心,则
ABC的边AB,BC,CA的中点,O是△ABC的重心,则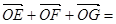 ( )
( )



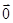
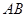 为圆
为圆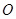 的直径,点
的直径,点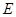 、
、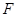 在圆
在圆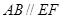 ,矩形
,矩形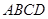 所在的平面与圆
所在的平面与圆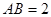 ,
,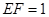 .
.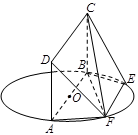
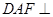 平面
平面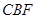 ;
;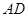 的长为何值时,平面
的长为何值时,平面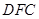 与平面
与平面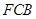 所成的锐二面角的大小为
所成的锐二面角的大小为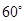 ?
?

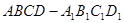 中,
中, 是棱
是棱 的中点.
的中点.
 平面
平面 ;
; .
.