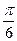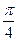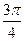题目内容
已知△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c.
向量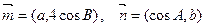 满足
满足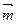 ∥
∥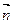 .(1)求sinA+sinB的取值范围;
.(1)求sinA+sinB的取值范围;
(2)若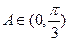 ,且实数x满足
,且实数x满足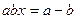 ,试确定x的取值范围.
,试确定x的取值范围.
向量
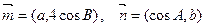 满足
满足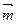 ∥
∥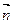 .(1)求sinA+sinB的取值范围;
.(1)求sinA+sinB的取值范围;(2)若
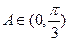 ,且实数x满足
,且实数x满足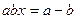 ,试确定x的取值范围.
,试确定x的取值范围.(1) 1<sinA+sin B≤,
B≤,
(2)(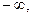
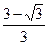 )
)
 B≤,
B≤,(2)(
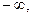
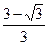 )
)(1)因为m∥n,所以=,即ab=4cosAcosB.
因为△ABC的外接圆半径 为1,由正弦定理,得ab=4sinAsinB.
为1,由正弦定理,得ab=4sinAsinB.
于是cosAcosB-sinAsinB=0,即cos(A+B)=0.
因为0<A+B<π.所以A+B=.故△ABC为直角三角形.
sinA+sinB=sinA+cosA=sin(A+),因为<A+<,
所以<sin(A +)≤1,故1<sinA+sin
+)≤1,故1<sinA+sin B≤.
B≤.
(2)x=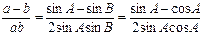 .
.
设t=sinA-cosA(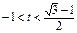 ),
),
则2sinAcosA=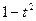 ,
,
x=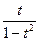 ,因为x′=
,因为x′=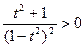 ,
,
故x=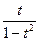 在(
在(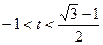 )上是单调递增函数.
)上是单调递增函数.
所以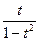
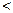
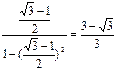
所以实数x的取值范围是(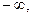
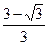 ).
).
因为△ABC的外接圆半径
 为1,由正弦定理,得ab=4sinAsinB.
为1,由正弦定理,得ab=4sinAsinB.于是cosAcosB-sinAsinB=0,即cos(A+B)=0.
因为0<A+B<π.所以A+B=.故△ABC为直角三角形.
sinA+sinB=sinA+cosA=sin(A+),因为<A+<,
所以<sin(A
 +)≤1,故1<sinA+sin
+)≤1,故1<sinA+sin B≤.
B≤.(2)x=
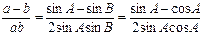 .
.设t=sinA-cosA(
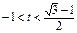 ),
),则2sinAcosA=
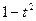 ,
,x=
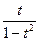 ,因为x′=
,因为x′=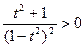 ,
,故x=
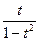 在(
在(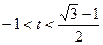 )上是单调递增函数.
)上是单调递增函数.所以
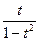
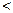
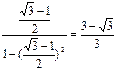
所以实数x的取值范围是(
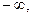
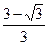 ).
).

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
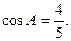
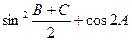 的值;(6分)
的值;(6分) 的值(6分)
的值(6分)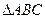 中,角
中,角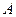 、
、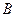 、
、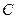 所对的边分别为
所对的边分别为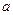 、
、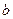 、
、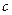 ,且
,且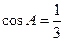 (1)求
(1)求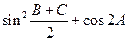 的值;
的值;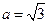 ,求
,求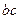 的最大值。
的最大值。
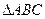 中,
中,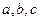 分别是角
分别是角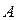 ,
,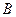 ,
,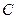 所对边的长,
所对边的长,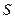 是
是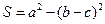 ,求
,求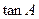 的值. (10分)
的值. (10分) ABC中,a.b.c分别为角A.B.C的对边,且:
ABC中,a.b.c分别为角A.B.C的对边,且: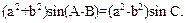
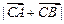 的值.
的值.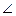 C=60°,
C=60°, 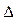 ABC面积为
ABC面积为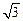 .求
.求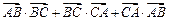 的值.
的值.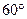 ,另两边之比为8:5,则这个三角形的面积为_________
,另两边之比为8:5,则这个三角形的面积为_________ 中,
中, ,
, ,
, ,那么角
,那么角 等于 ( )
等于 ( ) 或
或


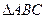 中,
中,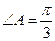 ,
,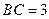 ,
,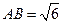 ,则
,则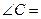 ( )
( )