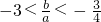题目内容
设函数 ,且
,且 ,
, ,则下列结论不正确 的是( )
,则下列结论不正确 的是( )A.a>0且b<0
B.

C.

D.

【答案】分析:求导,由f′(1)=- 得
得 a+b+c=0,结合b<c<
a+b+c=0,结合b<c< a得a>0且b<0,用等式可消去一个量,用不等式组求其它两个量的比值.
a得a>0且b<0,用等式可消去一个量,用不等式组求其它两个量的比值.
解答:解:∵f′(x)=ax2+bx+c,∴f′(1)=a+b+c=- ,
,
∴ a+b+c=0,又b<c<
a+b+c=0,又b<c< a=0,∴a>0且b<0,∴A正确,
a=0,∴a>0且b<0,∴A正确,
把c=- a-b代入b<c<
a-b代入b<c< a得-3a<b<-
a得-3a<b<- a∴-3<
a∴-3< <-
<- ,∴B正确,
,∴B正确,
把 a=-b-c代入b<c<
a=-b-c代入b<c< a得b<c<-
a得b<c<- b∴-
b∴- <
< <1,∴C正确,
<1,∴C正确,
把b=- a-c代入b<c<
a-c代入b<c< a得-
a得- a<c<
a<c< a∴-
a∴- <
< <
< ,∴D错误.
,∴D错误.
故选D.
点评:本题考查导数的运算,不等式与不等关系等知识点,求两个量的比值时注意把不等式转化为不等式组,考查学生的基本运算能力.
 得
得 a+b+c=0,结合b<c<
a+b+c=0,结合b<c< a得a>0且b<0,用等式可消去一个量,用不等式组求其它两个量的比值.
a得a>0且b<0,用等式可消去一个量,用不等式组求其它两个量的比值.解答:解:∵f′(x)=ax2+bx+c,∴f′(1)=a+b+c=-
 ,
,∴
 a+b+c=0,又b<c<
a+b+c=0,又b<c< a=0,∴a>0且b<0,∴A正确,
a=0,∴a>0且b<0,∴A正确,把c=-
 a-b代入b<c<
a-b代入b<c< a得-3a<b<-
a得-3a<b<- a∴-3<
a∴-3< <-
<- ,∴B正确,
,∴B正确,把
 a=-b-c代入b<c<
a=-b-c代入b<c< a得b<c<-
a得b<c<- b∴-
b∴- <
< <1,∴C正确,
<1,∴C正确,把b=-
 a-c代入b<c<
a-c代入b<c< a得-
a得- a<c<
a<c< a∴-
a∴- <
< <
< ,∴D错误.
,∴D错误.故选D.
点评:本题考查导数的运算,不等式与不等关系等知识点,求两个量的比值时注意把不等式转化为不等式组,考查学生的基本运算能力.

练习册系列答案
相关题目
 ,且
,且 ,
, ,
, ,下列命题:
,下列命题: ,则
,则
 ,
, ,使得
,使得
 ,
, ,则
,则
 ,都有
,都有
 ,且
,且 ,
, ,则下列结论中不正确的是
,则下列结论中不正确的是 C.
C. C.
C. D.
D.
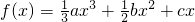 ,且
,且 ,
, ,则下列结论不正确 的是
,则下列结论不正确 的是