题目内容
【题目】已知在四棱锥P﹣ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点. 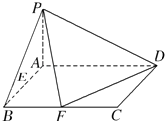
(Ⅰ)证明:PF⊥FD;
(Ⅱ)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(Ⅲ)若PB与平面ABCD所成的角为45°,求二面角A﹣PD﹣F的余弦值.
【答案】解:解法一:(Ⅰ)∵PA⊥平面ABCD,∠BAD=90°,AB=1,AD=2,建立如图所示的空间直角坐标系A﹣xyz, 则A(0,0,0),B(1,0,0),F(1,1,0),D(0,2,0).
不妨令P(0,0,t)∵ ![]() ,
, ![]()
∴ ![]() ,
,
即PF⊥FD.
(Ⅱ)设平面PFD的法向量为 ![]() ,
,
由 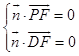 ,得
,得 ![]() ,令z=1,解得:
,令z=1,解得: ![]() .
.
∴ ![]() .
.
设G点坐标为(0,0,m), ![]() ,则
,则 ![]() ,
,
要使EG∥平面PFD,只需 ![]() ,即
,即 ![]() ,
,
得 ![]() ,从而满足
,从而满足 ![]() 的点G即为所求.
的点G即为所求.
(Ⅲ)∵AB⊥平面PAD,
∴ ![]() 是平面PAD的法向量,易得
是平面PAD的法向量,易得 ![]() ,
,
又∵PA⊥平面ABCD,
∴∠PBA是PB与平面ABCD所成的角,
得∠PBA=45°,PA=1,平面PFD的法向量为 ![]()
∴ 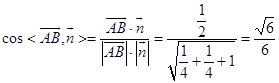 ,
,
故所求二面角A﹣PD﹣F的余弦值为 ![]() .
.
解法二:(Ⅰ)证明:连接AF,则 ![]() ,
, ![]() ,
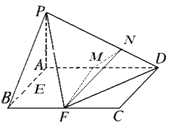
,
又AD=2,∴DF2+AF2=AD2 ,
∴DF⊥AF(2分)
又PA⊥平面ABCD,
∴DF⊥PA,又PA∩AF=A,
∴ 
(Ⅱ)过点E作EH∥FD交AD于点H,则EH∥平面PFD,且有 ![]()
再过点H作HG∥DP交PA于点G,则HG∥平面PFD且 ![]() ,
,
∴平面GEH∥平面PFD
∴EG∥平面PFD.
从而满足 ![]() 的点G即为所求
的点G即为所求
(Ⅲ)∵PA⊥平面ABCD,
∴∠PBA是PB与平面ABCD所成的角,且∠PBA=45°.
∴PA=AB=1
取AD的中点M,则FM⊥AD,FM⊥平面PAD,在平面PAD中,过M作MN⊥PD于N,连接FN,则PD⊥平面FMN,则∠MNF即为二面角A﹣PD﹣F的平面角
∵Rt△MND∽Rt△PAD,
∴ ![]() ,
,
∵ ![]() ,且∠FMN=90°
,且∠FMN=90°
∴ ![]() ,
, ![]() ,
,
∴ ![]()
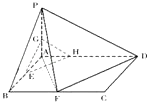
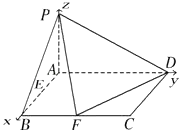
【解析】解法一(向量法)(I)建立如图所示的空间直角坐标系A﹣xyz,分别求出直线PF与FD的平行向量,然后根据两个向量的数量积为0,得到PF⊥FD;(Ⅱ)求出平面PFD的法向量(含参数t),及EG的方向向量,进而根据线面平行,则两个垂直数量积为0,构造方程求出t值,得到G点位置;(Ⅲ)由 ![]() 是平面PAD的法向量,根据PB与平面ABCD所成的角为45°,求出平面PFD的法向量,代入向量夹角公式,可得答案. 解法二(几何法)(I)连接AF,由勾股定理可得DF⊥AF,由PA⊥平面ABCD,由线面垂直性质定理可得DF⊥PA,再由线面垂直的判定定理得到DF⊥平面PAF,再由线面垂直的性质定理得到PF⊥FD;(Ⅱ)过点E作EH∥FD交AD于点H,则EH∥平面PFD,且有
是平面PAD的法向量,根据PB与平面ABCD所成的角为45°,求出平面PFD的法向量,代入向量夹角公式,可得答案. 解法二(几何法)(I)连接AF,由勾股定理可得DF⊥AF,由PA⊥平面ABCD,由线面垂直性质定理可得DF⊥PA,再由线面垂直的判定定理得到DF⊥平面PAF,再由线面垂直的性质定理得到PF⊥FD;(Ⅱ)过点E作EH∥FD交AD于点H,则EH∥平面PFD,且有 ![]() ,再过点H作HG∥DP交PA于点G,则HG∥平面PFD且
,再过点H作HG∥DP交PA于点G,则HG∥平面PFD且 ![]() ,由面面平行的判定定理可得平面GEH∥平面PFD,进而由面面平行的性质得到EG∥平面PFD.从而确定G点位置;(Ⅲ)由PA⊥平面ABCD,可得∠PBA是PB与平面ABCD所成的角,即∠PBA=45°,取AD的中点M,则FM⊥AD,FM⊥平面PAD,在平面PAD中,过M作MN⊥PD于N,连接FN,则PD⊥平面FMN,则∠MNF即为二面角A﹣PD﹣F的平面角,解三角形MNF可得答案.
,由面面平行的判定定理可得平面GEH∥平面PFD,进而由面面平行的性质得到EG∥平面PFD.从而确定G点位置;(Ⅲ)由PA⊥平面ABCD,可得∠PBA是PB与平面ABCD所成的角,即∠PBA=45°,取AD的中点M,则FM⊥AD,FM⊥平面PAD,在平面PAD中,过M作MN⊥PD于N,连接FN,则PD⊥平面FMN,则∠MNF即为二面角A﹣PD﹣F的平面角,解三角形MNF可得答案.
【考点精析】通过灵活运用空间中直线与直线之间的位置关系和直线与平面平行的判定,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.