题目内容
若x，y∈R，A={（x，y）|y=x}，B={（x，y）|| y | x |
分析：根据集合A，B表示的几何图形，来确定两个集合之间的关系．
解答：解：A={（x，y）|y=x}表示直线y=x上点的集合，
B={（x，y）|
=1}表示直线y=x除（0，0）之外的点的集合；
故B⊆A，
故答案为B⊆A．
B={（x，y）|
| y |
| x |
故B⊆A，
故答案为B⊆A．
点评：本题是基础题，考查函数图象之间关系，集合的子集问题，明确函数的图象的特征，是解好本题的根据．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
如图所示的韦恩图中，A、B是非空集合，定义A*B表示阴影部分的集合．若x，y∈R，A={x|y=
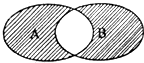如图所示的韦恩图中，A，B是非空集合，定义集合A#B为阴影部分表示的集合．若x，y∈R，A={x|y=| 2x-x2 |
| A、{x|0＜x＜2} |
| B、{x|1＜x≤2} |
| C、{x|0≤x≤1或x≥2} |
| D、{x|0≤x≤1或x＞2} |
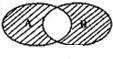如图所示的韦恩图中，A、B是非空集合，定义A*B表示阴影部分的集合．若x，y∈R，A={y|y=x2}，B={x|x=y+1，y＞0}，则A*B为
（2013•牡丹江一模）如图所示的韦恩图中，A、B是非空集合，定义A*B表示阴影部分集合．若x，y∈R，