题目内容
从某校参加高一年级基础知识数学测试的450名同学中,随机抽取若干名同学,将他们的成绩制成如下频率分布表.
(1)根据表中已知数据,填写在①、②、③处的数值分别为 ( ),( ),( );
(2)补全在区间[90,160]上的频率分布直方图;
(3)请你估计该校成绩不低于130分的同学人数.
(1)根据表中已知数据,填写在①、②、③处的数值分别为 ( ),( ),( );
(2)补全在区间[90,160]上的频率分布直方图;
(3)请你估计该校成绩不低于130分的同学人数.

解:(1)根据在[120,130)上的频数为16,频率为0.32可知:一共抽 =50人
=50人
在[140,150)上的频数为2,则频率= =0.04
=0.04
根据频率和等于1可知:
在[100,110)上的频率为:1﹣(0.08+0.36+0.32+0.08+0.04+0.02)=0.1
故答案为:0.04,0.10,50
(2)求出每组的 ,即为矩形的高,画出下图
,即为矩形的高,画出下图

(3)在随机抽取的50名学生中有7名不低于13.450× =63.
=63.
答:450名学生中不低于130(分)的大约有63名.
 =50人
=50人在[140,150)上的频数为2,则频率=
 =0.04
=0.04根据频率和等于1可知:
在[100,110)上的频率为:1﹣(0.08+0.36+0.32+0.08+0.04+0.02)=0.1
故答案为:0.04,0.10,50
(2)求出每组的
 ,即为矩形的高,画出下图
,即为矩形的高,画出下图
(3)在随机抽取的50名学生中有7名不低于13.450×
 =63.
=63.答:450名学生中不低于130(分)的大约有63名.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
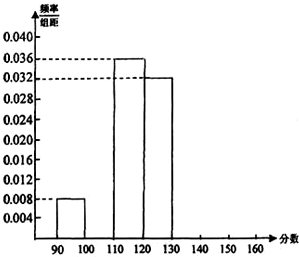 从某校参加高一年级基础知识数学测试的450名同学中,随机抽取若干名同学,将他们的成绩制成如下频率分布表.
从某校参加高一年级基础知识数学测试的450名同学中,随机抽取若干名同学,将他们的成绩制成如下频率分布表.(1)根据表中已知数据,填写在①、②、③处的数值分别为
(2)补全在区间[90,160]上的频率分布直方图;
(3)请你估计该校成绩不低于130分的同学人数.
| 分组 | 频数 | 频率 |
| [90,100) | 0.08 | |
| [100,110) | ② | |
| [110,120) | 0.36 | |
| [120,130) | 16 | 0.32 |
| [130,140) | 0.O8 | |
| [140,150) | 2 | ① |
| [150,160] | 0.O2 | |
| 合计 | ③ |
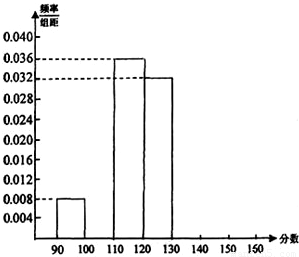 从某校参加高一年级基础知识数学测试的450名同学中,随机抽取若干名同学,将他们的成绩制成如下频率分布表.
从某校参加高一年级基础知识数学测试的450名同学中,随机抽取若干名同学,将他们的成绩制成如下频率分布表.(1)根据表中已知数据,填写在①、②、③处的数值分别为______,______,______;
(2)补全在区间[90,160]上的频率分布直方图;
(3)请你估计该校成绩不低于130分的同学人数.
| 分组 | 频数 | 频率 |
| [90,100) | 0.08 | |
| [100,110) | ② | |
| [110,120) | 0.36 | |
| [120,130) | 16 | 0.32 |
| [130,140) | 0.O8 | |
| [140,150) | 2 | ① |
| [150,160] | 0.O2 | |
| 合计 | ③ |


