题目内容
 若函数f(x)=
若函数f(x)=| (1-2a)x |
| 2(x2+a) |
| A、(1,+∞) | ||
| B、(0,1) | ||
C、(0,
| ||
D、(-∞,
|
分析:结合函数的图象并利用导函数的性质得a>0,再结合图象在第一象限内的性质得出1-2a>0,即可解答.
解答:解:∵函数f(x)=
,
∴f′(x)=
,令f′(x)=0得:x2=a
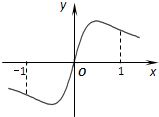
由图可知,函数f(x)有两个极值点,
故方程:x2=a有实数解,∴a>0.
又从图象中得出,当x>0时,y>0,
∴1-2a>0,
∴a<
故a∈(0,
).
故选C.
| (1-2a)x |
| 2(x2+a) |
∴f′(x)=
| (1-2a)(a-x 2) |
| 2(x2+a) 2 |
由图可知,函数f(x)有两个极值点,
故方程:x2=a有实数解,∴a>0.
又从图象中得出,当x>0时,y>0,
∴1-2a>0,
∴a<
| 1 |
| 2 |
故a∈(0,
| 1 |
| 2 |
故选C.
点评:本题考查了函数的图象、函数的极值与导数的联系,函数值与对应自变量取值范围的关系,解答关键是需要形数结合解题.

练习册系列答案
相关题目