题目内容
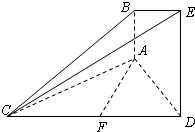 (2013•永州一模)如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2013•永州一模)如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.(1)求证:AF∥平面BCE;
(2)求直线CE与平面ADE所成角的正弦值.
分析:(1)取CE的中点G,连结FG,BG,先证明四边形GFAB为平行四边形,可得AF∥BG,再利用线面平行的判定方法,即可证明结论;
(2)取AD的中点H,连结CH,EH,证明∠CEH为CE与平面ADE所成角,再利用正弦函数即可求得.
(2)取AD的中点H,连结CH,EH,证明∠CEH为CE与平面ADE所成角,再利用正弦函数即可求得.
解答: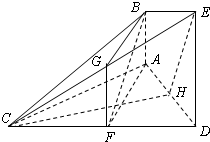 (1)证明:取CE的中点G,连结FG,BG.
(1)证明:取CE的中点G,连结FG,BG.
∵F为CD的中点,
∴GF∥DE且GF=
DE.
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,
∴GF∥AB. …(2分)
又AB=
DE,∴GF=AB.
∴四边形GFAB为平行四边形,∴AF∥BG …(4分)
∵AF?平面BCE,BG?平面BCE,
∴AF∥平面BCE. …(6分)
(2)解:取AD的中点H,连结CH,EH.
∵△ACD为等边三角形,∴CH⊥AD
又DE⊥平面ACD,CH?面ACD
∴CH⊥DE
∵AD∩DE=D
∴CH⊥平面ADE
∴∠CEH为CE与平面ADE所成角.…(8分)
不妨设AD=2,则DE=CD=2,CE=2
,CH=
.
在Rt△CHE中,sin∠CEH=
=
∴直线CE与面ADE所成角的正弦值为
.…(12分)
 (1)证明:取CE的中点G,连结FG,BG.
(1)证明:取CE的中点G,连结FG,BG.∵F为CD的中点,
∴GF∥DE且GF=
| 1 |
| 2 |
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,
∴GF∥AB. …(2分)
又AB=
| 1 |
| 2 |
∴四边形GFAB为平行四边形,∴AF∥BG …(4分)
∵AF?平面BCE,BG?平面BCE,
∴AF∥平面BCE. …(6分)
(2)解:取AD的中点H,连结CH,EH.
∵△ACD为等边三角形,∴CH⊥AD
又DE⊥平面ACD,CH?面ACD
∴CH⊥DE
∵AD∩DE=D
∴CH⊥平面ADE
∴∠CEH为CE与平面ADE所成角.…(8分)
不妨设AD=2,则DE=CD=2,CE=2
| 2 |
| 3 |
在Rt△CHE中,sin∠CEH=
| CH |
| CE |
| ||
| 4 |
∴直线CE与面ADE所成角的正弦值为
| ||
| 4 |
点评:本题考查线面平行,考查线面角,考查学生的计算能力,考查学生分析解决问题的能力,掌握线面平行的判定方法是关键.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目