题目内容
二次函数f(x),又y=f(x)-
的图象与x轴有且仅有一个公共点,且f′(x)=1-2x.
(1)求f(x)的表达式.
(2)若直线y=kx把y=f(x)的图象与x轴所围成的图形的面积二等分,求k的值.
| 1 | 4 |
(1)求f(x)的表达式.
(2)若直线y=kx把y=f(x)的图象与x轴所围成的图形的面积二等分,求k的值.
分析:(1)由题意设f(x)=ax2+bx+c,求出f′(x)后结合题意求出a、b,再代入y=f(x)-
化简,由题意和二次函数的性质令△=0求出c的值,代入解析式求出f(x);
(2)先求出f(x)=x-x2图象与x轴交点坐标,再画出图象,并求出y=kx和y=f(x)的图象的交点的横坐标,结合题意和定积分知识列出方程,求出k的值.
| 1 |
| 4 |
(2)先求出f(x)=x-x2图象与x轴交点坐标,再画出图象,并求出y=kx和y=f(x)的图象的交点的横坐标,结合题意和定积分知识列出方程,求出k的值.
解答:解:(1)设f(x)=ax2+bx+c,则f′(x)=2ax+b,
∵f′(x)=1-2x,∴a=-1,b=1,
∴y=f(x)-
=-x2+x+c-
的图象与x轴有且仅有一个公共点,
∴△=1+4(c-
)=0,解得c=0,
则f(x)=x-x2….
(2)由(1)得f(x)=x-x2图象与x轴交点是(0,0)、(1,0),
如图: 直线y=kx和y=f(x)的图象的交点为A,
直线y=kx和y=f(x)的图象的交点为A,
由
得,x=1-k,
∵直线y=kx把y=f(x)的图象与x轴所围成的图形的面积二等分,
∴
(x-x2)dx=
(x-x2-kx)dx,
即
×(
-
)=
×(1-k)2-
×(1-k)3,
=
,解得k=1-
,
故k的值是1-
.
∵f′(x)=1-2x,∴a=-1,b=1,
∴y=f(x)-
| 1 |
| 4 |
| 1 |
| 4 |
∴△=1+4(c-
| 1 |
| 4 |
则f(x)=x-x2….
(2)由(1)得f(x)=x-x2图象与x轴交点是(0,0)、(1,0),
如图:
 直线y=kx和y=f(x)的图象的交点为A,
直线y=kx和y=f(x)的图象的交点为A,由
|
∵直线y=kx把y=f(x)的图象与x轴所围成的图形的面积二等分,
∴
| 1 0 |
| ∫ | 1-k 0 |
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1-k |
| 2 |
| 1 |
| 3 |
| 1 |
| 12 |
| (1-k)3 |
| 6 |
| |||
| 2 |
故k的值是1-
| |||
| 2 |
点评:本题考查了二次函数的性质,待定系数法求解析式,以及定积分求不规则图形的面积问题,关键是正确画图和确定积分的上界和下界,属于中档题.

练习册系列答案
相关题目
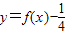 的图象与x轴有且仅有一个公共点,且f′(x)=1-2x.
的图象与x轴有且仅有一个公共点,且f′(x)=1-2x.