题目内容
已知函数f(x)=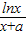 ( a为常数)在点(1,f(1))处切线的斜率为
( a为常数)在点(1,f(1))处切线的斜率为 .
.(Ⅰ)求实数a的值;
(Ⅱ)若函数f(x)在区间[t,+∞)(t∈Z)上存在极值,求t的最大值.
【答案】分析:(Ⅰ)求导数,函数f(x)在点(1,f(1))处切线的斜率为 ,可得
,可得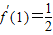 ,解之即可;(Ⅱ)把问题转化为方程
,解之即可;(Ⅱ)把问题转化为方程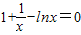 在[t,+∞)(t∈Z)上有解,构造函数
在[t,+∞)(t∈Z)上有解,构造函数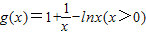 ,可得函数g(x)有零点x∈(3,4),进而可得答案.
,可得函数g(x)有零点x∈(3,4),进而可得答案.
解答:解:(Ⅰ)求导数可得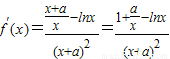 ,
,
∵函数f(x)在点(1,f(1))处切线的斜率为 ,
,
∴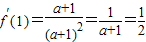 ,解得a=1---------------------------------(5分)
,解得a=1---------------------------------(5分)
(Ⅱ)由(I)可知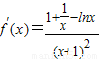
∵函数f(x)在区间[t,+∞)(t∈Z)上存在极值,
∴方程f′(x)=0 在[t,+∞)(t∈Z)上有解,
∴方程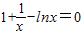 在[t,+∞)(t∈Z)上有解----------------------------------(7分)
在[t,+∞)(t∈Z)上有解----------------------------------(7分)
令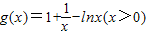 ,
,
∵x>0,∴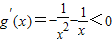 ,
,
∴g(x)在(0,+∞)上为减函数---(9分)
又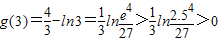 ,
,
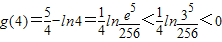
∴函数g(x)有零点x∈(3,4)----------------------------------(12分)
∵方程g(x)=0在[t,+∞)上有解,且t∈Z,
∴t≤3,∴t的最大值为3.---------(13分)
点评:本题为函数与导数的综合应用,涉及切线问题和构造函数法以及函数的零点,属中档题.
 ,可得
,可得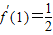 ,解之即可;(Ⅱ)把问题转化为方程
,解之即可;(Ⅱ)把问题转化为方程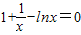 在[t,+∞)(t∈Z)上有解,构造函数
在[t,+∞)(t∈Z)上有解,构造函数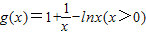 ,可得函数g(x)有零点x∈(3,4),进而可得答案.
,可得函数g(x)有零点x∈(3,4),进而可得答案.解答:解:(Ⅰ)求导数可得
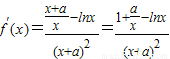 ,
,∵函数f(x)在点(1,f(1))处切线的斜率为
 ,
,∴
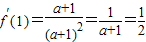 ,解得a=1---------------------------------(5分)
,解得a=1---------------------------------(5分)(Ⅱ)由(I)可知
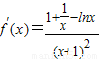
∵函数f(x)在区间[t,+∞)(t∈Z)上存在极值,
∴方程f′(x)=0 在[t,+∞)(t∈Z)上有解,
∴方程
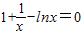 在[t,+∞)(t∈Z)上有解----------------------------------(7分)
在[t,+∞)(t∈Z)上有解----------------------------------(7分)令
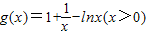 ,
,∵x>0,∴
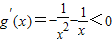 ,
,∴g(x)在(0,+∞)上为减函数---(9分)
又
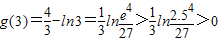 ,
,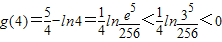
∴函数g(x)有零点x∈(3,4)----------------------------------(12分)
∵方程g(x)=0在[t,+∞)上有解,且t∈Z,
∴t≤3,∴t的最大值为3.---------(13分)
点评:本题为函数与导数的综合应用,涉及切线问题和构造函数法以及函数的零点,属中档题.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|