题目内容
如图,正方形的边长为6,E为AD上一点,以AB所在直线为轴将正方形旋转一周,由△ACE与△DCE旋转所得几何体的体积相等,试确定E的位置.
思路解析:判断旋转体的形体与平面图形及轴是相关的.只有明确形体才能建立相关体积的关系式,从而引进未知量,求得结果.
解:设AE=x,且△ABC绕AB旋转一周所得圆锥的体积为V0,直角梯形ABCE绕AB旋转一周所得圆台的体积为V1,正方形ABCD绕AB旋转一周所得圆柱的体积为V2.由已知有V1-V0=V2-V1,即V0+V2=2V1,亦即π×62×6+![]() ×62×6=2×
×62×6=2×![]() ×6×(πx2+36π+6πx).
×6×(πx2+36π+6πx).
整理,得x2+6x-36=0.
解得x=-3-3![]() (舍)或x=-3+3
(舍)或x=-3+3![]() .
.
∴![]() .
.
故AE=-3+3![]() (或E为黄金分割点).
(或E为黄金分割点).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的边长为
的边长为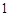 ,
,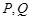 分别为边
分别为边 上的点,当
上的点,当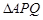 的周长为
的周长为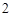 时,求
时,求 的大小.
的大小.
 的边长为
的边长为 ,它是水平放置的一个平面图形的直观图,则原图形的周长是
,它是水平放置的一个平面图形的直观图,则原图形的周长是


 的边长为
的边长为 ,它是水平放置的一个平面图形的直观图,则原图形的周长是
,它是水平放置的一个平面图形的直观图,则原图形的周长是 