题目内容
已知函数f(x)=log3(ax+b)的图象过点A(2,1),B(5,2),
(1)求函数f(x)的解析式;
(2)记an=3f(n)(n∈N*),是否存在正数k,使得 对一切n∈N*均成立,若存在,求出k的最大值;若不存在,说明理由。
对一切n∈N*均成立,若存在,求出k的最大值;若不存在,说明理由。
(1)求函数f(x)的解析式;
(2)记an=3f(n)(n∈N*),是否存在正数k,使得
 对一切n∈N*均成立,若存在,求出k的最大值;若不存在,说明理由。
对一切n∈N*均成立,若存在,求出k的最大值;若不存在,说明理由。解:(1)由已知得,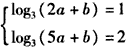 ,解得a=2,b=-1,
,解得a=2,b=-1,
所以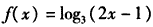 。
。
(2)由题知,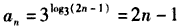 ,
,
假设存在正数k使得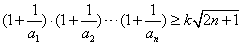 对一切n∈N*均成立,
对一切n∈N*均成立,
则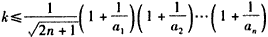 ,
,
记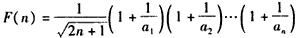 ,
,
则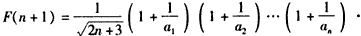
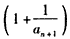 ,
,
∵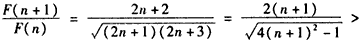
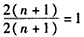 ,
,
∴F(n+1)>F(n),所以{F(n)}是递增数列,
∵n∈N*,
∴当n=1时F(n)最小,最小值为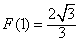 ,
,
∴k≤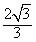 ,即k的最大值为
,即k的最大值为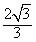 。
。
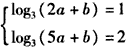 ,解得a=2,b=-1,
,解得a=2,b=-1,所以
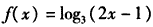 。
。 (2)由题知,
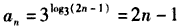 ,
,假设存在正数k使得
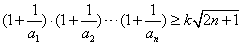 对一切n∈N*均成立,
对一切n∈N*均成立,则
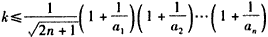 ,
,记
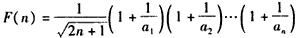 ,
,则
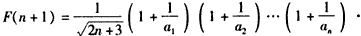
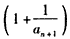 ,
,∵
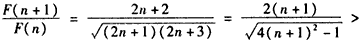
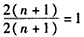 ,
,∴F(n+1)>F(n),所以{F(n)}是递增数列,
∵n∈N*,
∴当n=1时F(n)最小,最小值为
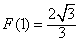 ,
,∴k≤
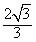 ,即k的最大值为
,即k的最大值为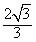 。
。 
练习册系列答案
相关题目