题目内容
在各项均为正数的等比数列 中,公比
中,公比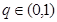 .若
.若 ,
, 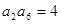 ,
, 数列
数列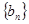 的前
的前 项和为
项和为 ,则当
,则当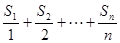 取最大值时,
取最大值时, 的值为( )
的值为( )
| A.8 | B.9 | C.8或9 | D.17 |
C
解析试题分析:依题意有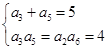 ,解得
,解得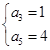 或
或 ,所以
,所以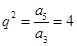 或
或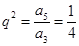 ,而
,而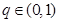 ,所以
,所以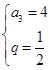 即
即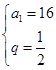 ,所以
,所以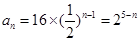 ,所以
,所以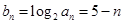 ,所以数列
,所以数列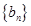 是以4为首项,
是以4为首项,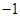 为公差的等差数列,所以
为公差的等差数列,所以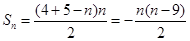 ,所以
,所以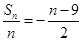 ,所以数列
,所以数列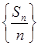 是以
是以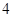 为首项,
为首项,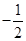 为公差的等差数列,要使
为公差的等差数列,要使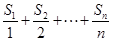 取得最大值,则必须是数列
取得最大值,则必须是数列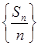 中所有正数项的和,才会取得最大值,所以由
中所有正数项的和,才会取得最大值,所以由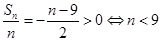 ,而
,而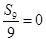 ,所以当
,所以当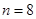 或
或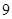 时,
时,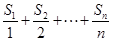 取得最大值,故选C.
取得最大值,故选C.
考点:1.等比数列的通项公式及其性质;2.等差数列的通项公式及其前 项和.
项和.

练习册系列答案
相关题目
等差数列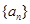 的公差
的公差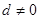 ,
,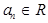 ,前
,前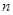 项和为
项和为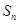 ,则对正整数
,则对正整数 ,下列四个结论中:
,下列四个结论中:
(1)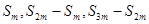 成等差数列,也可能成等比数列;
成等差数列,也可能成等比数列;
(2)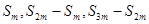 成等差数列,但不可能成等比数列;
成等差数列,但不可能成等比数列;
(3)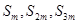 可能成等比数列,但不可能成等差数列;
可能成等比数列,但不可能成等差数列;
(4)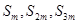 不可能成等比数列,也不可能成等差数列;
不可能成等比数列,也不可能成等差数列;
正确的是( )
| A.(1)(3). | B.(1)(4). | C.(2)(3). | D.(2)(4). |
在等差数列 中,若
中,若 ,则数列
,则数列 的通项公式为 ( )
的通项公式为 ( )
A. | B.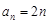 | C. | D.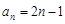 |
等差数列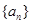 中,已知
中,已知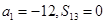 ,使得
,使得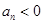 的最大正整数
的最大正整数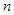 为( )
为( )
A.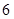 | B. | C. | D. |
等差数列前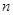 项和为
项和为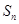 ,若
,若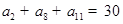 ,则
,则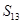 的值是( )
的值是( )
| A. 130 | B. 65 | C. 70 | D. 75 |
已知 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且 是
是 与
与 的等比中项,
的等比中项, 为
为 前
前 项和,
项和, 则
则 的值为( )
的值为( )
| A.-110 | B.-90 | C.90 | D.110 |
设等差数列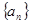 的前项和为
的前项和为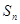 ,若
,若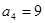 ,
,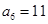 ,则
,则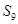 等于( )
等于( )
| A.180 | B.90 | C.72 | D.100 |
已知等差数列{an}的前n项和为Sn,满足a13=S13=13,则a1=( )
| A.-14 | B.13 | C.-12 | D.-11 |
在等差数列{an}中,首项a1=0,公差d≠0,若am=a1+a2+…+a9,则m的值为( )
| A.37 | B. 36 | C.20 | D.19 |