题目内容
14．
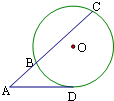如图，从圆O外一点A引圆的切线AD和割线ABC，已知AD=2$\sqrt{3}$，BC=2AB，圆心O到AC的距离为$\sqrt{5}$，则点A与圆O上的点的最短距离为$\sqrt{21}-3$．
分析 利用切割线定理，求出AB，然后利用勾股定理求解AO，求解圆的半径即可．
解答 解：由题意可知AD2=AB•AC=3AB2．AB=2，
圆心O到AC的距离为$\sqrt{5}$，则点A与圆O的距离为：$\sqrt{{4}^{2}+{（\sqrt{5}）}^{2}}$=$\sqrt{21}$．圆的半径为：$\sqrt{{（\sqrt{5}）}^{2}+{2}^{2}}$=3
点A与圆O上的点的最短距离为：$\sqrt{21}-3$．
故答案为：$\sqrt{21}-3$．
点评 本题考查圆的切线，切割线定理以及勾股定理的应用，考查计算能力．
练习册系列答案
相关题目
2．在区域$\left\{\begin{array}{l}0≤x≤1\\ 0≤y≤1\end{array}\right.$内任意取一点P（x，y），则x2+y2＞1的概率是（ ）
| A． | $\frac{2π-4}{4}$ | B． | $\frac{π-2}{4}$ | C． | $\frac{π}{4}$ | D． | $\frac{4-π}{4}$ |
9．
如图是某几何体的三视图（单位：cm），正视图是等腰梯形，俯视图中的曲线是两个同心的半圆，侧视图是直角梯形．则该几何体的体积等于（ ）
如图是某几何体的三视图（单位：cm），正视图是等腰梯形，俯视图中的曲线是两个同心的半圆，侧视图是直角梯形．则该几何体的体积等于（ ）| A． | 28 πcm3 | B． | 14πcm3 | C． | 7πcm3 | D． | 56πcm3 |
19．
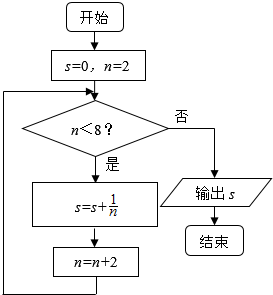如图所示，程序框图的输出结果是（ ）
如图所示，程序框图的输出结果是（ ）| A． | $\frac{1}{16}$ | B． | $\frac{25}{24}$ | C． | $\frac{11}{12}$ | D． | $\frac{3}{4}$ |
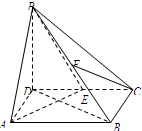如图，在四棱锥P-ABCD中，底面ABCD是矩形，AB=2，AD=$\sqrt{2}$，PD⊥平面ABCD，E，F分别为CD，PB的中点．求证：