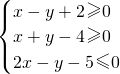题目内容
已知两实数x,y满足
求:(1)z=3x-2y的最大值;
(2)z=x2+y2-10y+25的最小值.
|
求:(1)z=3x-2y的最大值;
(2)z=x2+y2-10y+25的最小值.
分析:(1)画出约束条件表示的可行域,推出目标函数z=3x-2y经过的点,求出最大值.
(2)通过表达式的几何意义,判断最小值时的位置求出最值即可.
(2)通过表达式的几何意义,判断最小值时的位置求出最值即可.
解答: 解:(1)由约束条件
解:(1)由约束条件
表示的可行域如图,
直线2x-y-5=0与直线 x+y-4=0的交点(3,1)作直线3x-2y=0的平行线l,
当l经过(3,1)时,z取得最大值,3×3-2×1=7.
(2)由于z=x2+y2-10y+25=x2+(y-5)2,
z=x2+y2-10y+25的几何意义是点P(x,y)到点(0,5)的距离的平方,
所以z=x2+y2-10y+25的最小值为:原点到直线x-y+2=0的距离的平方:
d2=(
)2,
即z=x2+y2-10y+25的最小值zmin=
.
 解:(1)由约束条件
解:(1)由约束条件
|
表示的可行域如图,
直线2x-y-5=0与直线 x+y-4=0的交点(3,1)作直线3x-2y=0的平行线l,
当l经过(3,1)时,z取得最大值,3×3-2×1=7.
(2)由于z=x2+y2-10y+25=x2+(y-5)2,
z=x2+y2-10y+25的几何意义是点P(x,y)到点(0,5)的距离的平方,
所以z=x2+y2-10y+25的最小值为:原点到直线x-y+2=0的距离的平方:
d2=(
| |-5+2| | ||
|
即z=x2+y2-10y+25的最小值zmin=
| 9 |
| 2 |
点评:本题考查简单的线性规划的应用,表达式的几何意义是解题的关键,考查计算能力.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目