题目内容
已知圆M经过点(3,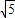 ),且圆心为(5,0),过坐标原点作其切线l.
),且圆心为(5,0),过坐标原点作其切线l.(Ⅰ)求圆M的方程;
(Ⅱ)求直线l的方程.
【答案】分析:(Ⅰ)法一:求出半径,然后求出圆M的标准方程;
法二:设出圆的标准方程,代入点的坐标,求出半径,求出圆的标准方程.
(Ⅱ)法一:求出OA的斜率然后求出直线l的方程.
法二:设出直线方程,利用直线与圆相切求出k即可求出直线方程.
解答:解:(Ⅰ)法一:点(3, )到圆心(5,0)的距离为圆的半径R,
)到圆心(5,0)的距离为圆的半径R,
所以 ..(2分)
..(2分)
所以圆的标准方程为(x-5)2+y2=9..(4分)
法二:设圆的标准方程为(x-5)2+y2=R2..(2分)
由圆M经过点(3, )得:
)得:
即:R2=9
所以圆的标准方程为(x-5)2+y2=R2..(4分)
(Ⅱ)法一:如图:直线OA、OB与圆M相切于
点A、B,由OM=5,AM=3
可知OA=4,所以 ..(6分)
..(6分)
由点斜式可得直线OA的方程为 ,同理可得直线OA方程为
,同理可得直线OA方程为 ..(8分)
..(8分)
法二:设切线方程为y=kx,与圆M方程联立方程组有唯一解,即: ⇒(1+k2)x2-10x+16=0有唯一解..(6分)
⇒(1+k2)x2-10x+16=0有唯一解..(6分)
所以:△=100-64(1+k2)=0,即:
所以所求切线方程为 ..(8分)
..(8分)
点评:本题是基础题,考查直线的切线方程,圆的标准方程,考查计算能力,常考题型.
法二:设出圆的标准方程,代入点的坐标,求出半径,求出圆的标准方程.
(Ⅱ)法一:求出OA的斜率然后求出直线l的方程.
法二:设出直线方程,利用直线与圆相切求出k即可求出直线方程.
解答:解:(Ⅰ)法一:点(3,
 )到圆心(5,0)的距离为圆的半径R,
)到圆心(5,0)的距离为圆的半径R,所以
 ..(2分)
..(2分)所以圆的标准方程为(x-5)2+y2=9..(4分)
法二:设圆的标准方程为(x-5)2+y2=R2..(2分)
由圆M经过点(3,
 )得:
)得:
即:R2=9
所以圆的标准方程为(x-5)2+y2=R2..(4分)
(Ⅱ)法一:如图:直线OA、OB与圆M相切于

点A、B,由OM=5,AM=3
可知OA=4,所以
 ..(6分)
..(6分)由点斜式可得直线OA的方程为
 ,同理可得直线OA方程为
,同理可得直线OA方程为 ..(8分)
..(8分)法二:设切线方程为y=kx,与圆M方程联立方程组有唯一解,即:
 ⇒(1+k2)x2-10x+16=0有唯一解..(6分)
⇒(1+k2)x2-10x+16=0有唯一解..(6分)所以:△=100-64(1+k2)=0,即:

所以所求切线方程为
 ..(8分)
..(8分)点评:本题是基础题,考查直线的切线方程,圆的标准方程,考查计算能力,常考题型.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目